题目内容
11．若2x+1＜0，求证：$\sqrt{4{x}^{2}-12x+9}$-$\sqrt{1+4x+4{x}^{2}}$=4．分析 首先得出2x-3＜0，进而化简二次根式得出即可．
解答 证明：∵2x+1＜0，
∴2x-3＜0，
∴$\sqrt{4{x}^{2}-12x+9}$-$\sqrt{1+4x+4{x}^{2}}$
=$\sqrt{（2x-3）^{2}}$-$\sqrt{（2x+1）^{2}}$
=-2x+3+2x+1
=4，
故$\sqrt{4{x}^{2}-12x+9}$-$\sqrt{1+4x+4{x}^{2}}$=4．
点评 此题主要考查了二次根式的性质与化简，正确化简二次根式是解题关键．
练习册系列答案
相关题目
1．已知x2-3x+1=0，则x4+$\frac{1}{x^{4}}$的值为（ ）
| A． | 7 | B． | 47 | C． | 9 | D． | 49 |
2．不等式组$\left\{\begin{array}{l}{x-3＜2}\\{x≥-1}\end{array}\right.$的解集是（ ）
| A． | x≥-1 | B． | x＜5 | C． | -1≤x＜5 | D． | x≤-1或x＞5 |
19．在一次学生田径运动会上，参加跳高的15名运动员的成绩如下表所示：
那么这些运动员跳高成绩的众数是（ ）
| 成绩（m） | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数 | 1 | 1 | 3 | 5 | 3 | 2 |
| A． | 3 | B． | 5 | C． | 1.65 | D． | 1.70 |
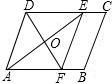如图，在?ABCD中，AE是∠DAB的平分线，EF∥AD交B于点F，连接DF交AE于点O，
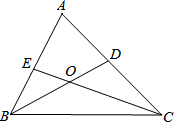如图，已知△ABC中，BD、CE分别是∠ABC、∠ACB的平分线，BD、CE交于点O．
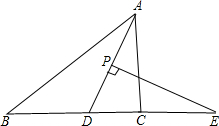在△ABC中，AD平分∠BAC，P为线段AD上的一个点，PE⊥AD交直线BC于点E（∠ABC、∠ACB的大小不确定）．