题目内容
19．已知点A（-4，0），B（2，0）．若点C在一次函数$y=\frac{1}{2}x+2$的图象上，且△ABC是直角三角形，则点C的个数是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据已知可求得直线与两轴的交点，分别过点B作垂线，可得出符合题意的点C．
解答 
解：由题意知，直线y=$\frac{1}{2}$x+2与x轴的交点为（-4，0），与y轴的交点为
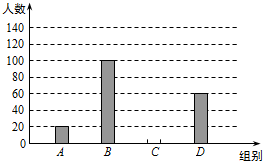
（0，2），如图：
过点B作BC垂直于直线于点C，作C′B⊥AB垂足为B，
故共有2个点能与点A，点B组成直角三角形．
故选：B．
点评 本题考查的是一次函数图象上点的坐标特点，熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
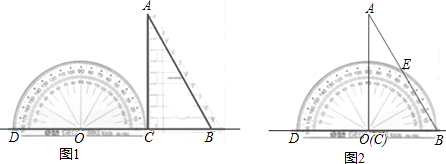
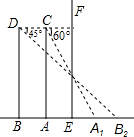如图所示，细心的王聪站立在镜子EF前的A处时，此时他看自己的脚在镜中的像A1的俯角为60°；如果王聪向后退0.3米到B处，这时他看自己的脚在镜中的像B1的俯角为45°．求王聪的眼睛到地面的距离BD．（结果精确到0.01米，参考数据：$\sqrt{3}≈1.73$）