题目内容
1.已知x2-3x+1=0,则x4+$\frac{1}{x^{4}}$的值为( )| A. | 7 | B. | 47 | C. | 9 | D. | 49 |
分析 先将x2-3x+1=0的两边同时除以x,再根据完全平方公式求出x2+$\frac{1}{{x}^{2}}$的值,进而可得出结论.
解答 解:∵x2-3x+1=0,
∴x+$\frac{1}{x}$=3,
∴(x+$\frac{1}{x}$)2=9,
∴x2+$\frac{1}{{x}^{2}}$=9-2=7,
∴(x2+$\frac{1}{{x}^{2}}$)2=49,
∴x4+$\frac{1}{x^{4}}$=49-2=47.
故选B.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.如果正多边形的一个内角等于135°,那么这个正多边形的边数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
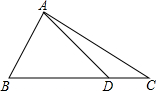 如图,在△ABC中,D是边BC上一点,BD=3DC,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{AD}$=$\frac{3}{4}$$\overrightarrow{b}$-$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示).
如图,在△ABC中,D是边BC上一点,BD=3DC,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{AD}$=$\frac{3}{4}$$\overrightarrow{b}$-$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$来表示).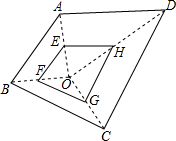 如图所示,E,F,G,H分别是OA,OB,OC,OD的中点,已知四边形EFGH的面积是3,则四边形ABCD的面积是( )
如图所示,E,F,G,H分别是OA,OB,OC,OD的中点,已知四边形EFGH的面积是3,则四边形ABCD的面积是( )