题目内容
6．
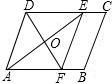如图，在?ABCD中，AE是∠DAB的平分线，EF∥AD交B于点F，连接DF交AE于点O，求证：四边形ADEF是菱形．
分析 首先证明四边形ADEF是平行四边形，然后根据角平分线的性质和平行线的性质证明∠AEF=∠EAF，根据等角对等边可得AF=EF，从而可得四边形ADEF是菱形．
解答 证明：∵四边形ABCD是平行四边形，
∴AB∥DC．
∵EF∥AD，
∴四边形ADEF是平行四边形，∠DAE=∠AEF．
∵AE是∠DAB的平分线，
∴∠DAE=∠EAF．
∴∠AEF=∠EAF．
∴AF=EF．
又∵四边形ADEF是平行四边形，
∴?ADEF是菱形．
点评 此题主要考查了菱形的判定，关键是掌握一组邻边相等的平行四边形是菱形．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
如图，A，B，C是⊙O上三点，已知∠ACB=α，则∠AOB=360°-2α．（用含α的式子表示）
1．
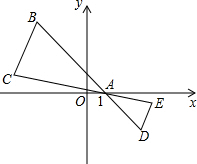如图，在△ABC中，B，C两个顶点在x轴的上方，点A的坐标是（1，0），以点A为位似图形，并把△ABC的边长缩小为原来的$\frac{1}{2}$倍，记所得的位似图形为△ADE．设点C的对应点E的横坐标为a，则点C的横坐标为（ ）
如图，在△ABC中，B，C两个顶点在x轴的上方，点A的坐标是（1，0），以点A为位似图形，并把△ABC的边长缩小为原来的$\frac{1}{2}$倍，记所得的位似图形为△ADE．设点C的对应点E的横坐标为a，则点C的横坐标为（ ）| A． | $\frac{1}{2}$（a-1） | B． | $\frac{1}{2}$（a+1） | C． | 3-2a | D． | 2（a-1） |
如图，EF⊥BC，DE⊥AB，∠B=∠ADE=30°．