题目内容
16.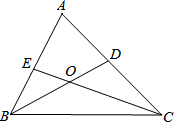 如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.
如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.(1)若∠A=50°,求∠BOC的度数;
(2)若∠A=n°,求∠BOC的度数.
分析 (1)根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠OBC+∠OCB,然后根据三角形的内角和定理列式计算即可得解;
(2)与(1)的思路相同求解即可.
解答 解:(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-∠A=180°-50°=130°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×130°=65°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°;
(2)∵∠A=n°,
∴∠ABC+∠ACB=180°-∠A=180°-n°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×(180°-n°)=90°-$\frac{1}{2}$n°,
在△OBC中,∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-$\frac{1}{2}$n°)=90°+$\frac{1}{2}$n°.
点评 本题考查了三角形的内角和定理,角平分线的定义,是基础题,要注意整体思想的利用.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
6.如果正多边形的一个内角等于135°,那么这个正多边形的边数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
7. 如图所示,图中共有相似三角形( )
如图所示,图中共有相似三角形( )
 如图所示,图中共有相似三角形( )
如图所示,图中共有相似三角形( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
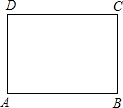 如图,在一张长为9cm,宽为8cm的矩形纸片上,现要剪下一个腰长为5cm的钝角等腰三角形,则剪下的钝角等腰三角形腰上的高为3或4cm,(要求:钝角等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上)
如图,在一张长为9cm,宽为8cm的矩形纸片上,现要剪下一个腰长为5cm的钝角等腰三角形,则剪下的钝角等腰三角形腰上的高为3或4cm,(要求:钝角等腰三角形的一个顶点与矩形的一个顶点重合,其余两个顶点在矩形的边上)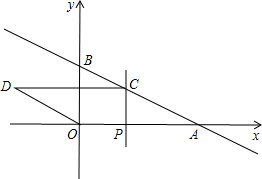 如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P为x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA、AC为边构造平行四边形OACD,设点P的横坐标为m.
如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P为x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA、AC为边构造平行四边形OACD,设点P的横坐标为m.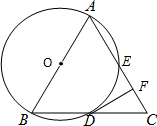 如图点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点,过D作AC的垂线,垂足为F.
如图点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点,过D作AC的垂线,垂足为F.