题目内容
11．
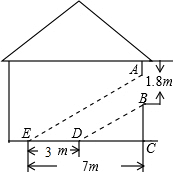如图，阳光通过窗口照到室内，在地上留下3m宽的亮区，已知亮区一边到窗下的墙角的距离CE=7m，窗口高AB=1.8m，那么窗口底边离地面的高BC等于（ ）| A． | 2m | B． | 2.4m | C． | 2.8m | D． | 3m |
分析 由太阳光线平行得到BD∥AE，则可判断△CBD∽△CAE，根据相似三角形的性质得$\frac{BC}{BC+1.8}$=$\frac{7-3}{7}$，然后利用比例的性质求BC即可．
解答 解：∵BD∥AE，
∴△CBD∽△CAE，
∴$\frac{BC}{CA}$=$\frac{CD}{CE}$，即$\frac{BC}{BC+1.8}$=$\frac{7-3}{7}$，
∴BC=2.4，
即窗口底边离地面的高BC等于2.4m．
故选B．
点评 本题考查了相似三角形的应用：利用太阳光线平行证明三角形相似，然后用相似三角形对应边的比相等的性质求物体的高度．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
用小立方块搭一个几何体，使得它的主视图和俯视图如图所示，搭这个几何体最少要多少个小立方块？并画出此时几何体的左视图（示意图）．
19．如果非零实数a是一元二次方程x2-5x+m=0的一个根，-a是方程x2+5x-m=0的一个根，那么a的值等于（ ）
| A． | 0 | B． | 1 | C． | $\frac{1}{2}$ | D． | 5 |
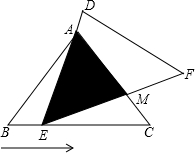如图，在△ABC中，已知AB=AC=3，BC=4，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF交于AC于M点．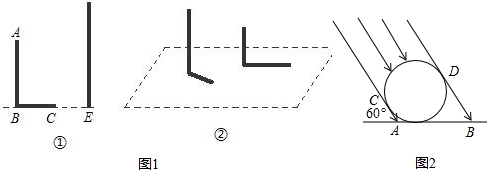
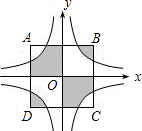如图，正方形ABCD的边长为4，其中它的中心与原点重合，AB∥x轴，BC∥y轴，反比例函数y=$\frac{2}{x}$与y=-$\frac{2}{x}$的图象均与正方形ABCD的边相交，则图中阴影面积的和是（ ）