题目内容
20.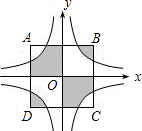 如图,正方形ABCD的边长为4,其中它的中心与原点重合,AB∥x轴,BC∥y轴,反比例函数y=$\frac{2}{x}$与y=-$\frac{2}{x}$的图象均与正方形ABCD的边相交,则图中阴影面积的和是( )
如图,正方形ABCD的边长为4,其中它的中心与原点重合,AB∥x轴,BC∥y轴,反比例函数y=$\frac{2}{x}$与y=-$\frac{2}{x}$的图象均与正方形ABCD的边相交,则图中阴影面积的和是( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 先根据两反比例函数的解析式确定出两函数图象之间的关系,再根据正方形ABCD的对称中心是坐标原点O可知图中四个小正方形全等,反比例函数的图象与两坐标轴所围成的图形全等,故阴影部分的面积即为两个小正方形即大正方形面积的一半.
解答 解:由两函数的解析可知:两函数的图象关于x轴对称.
∵正方形ABCD的对称中心是坐标原点O,
∴四个小正方形全等,
∴反比例函数的图象与两坐标轴所围成的图形全等,
∴阴影部分的面积=$\frac{1}{2}$S□ABCD=$\frac{1}{2}$×16=8.
故选:C.
点评 本题考查的是关于x轴对称的反比例函数解析式的特点,解答此题的关键是根据函数解析式判断出两函数图象的特点,再根据正方形的面积即可解答.

练习册系列答案
相关题目
11.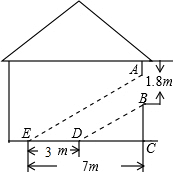 如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
 如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )| A. | 2m | B. | 2.4m | C. | 2.8m | D. | 3m |
5. 如图,∠A是⊙O的圆周角,∠A=52°,则∠BOC的度数为( )
如图,∠A是⊙O的圆周角,∠A=52°,则∠BOC的度数为( )
 如图,∠A是⊙O的圆周角,∠A=52°,则∠BOC的度数为( )
如图,∠A是⊙O的圆周角,∠A=52°,则∠BOC的度数为( )| A. | 100° | B. | 104° | C. | 102° | D. | 96° |
12.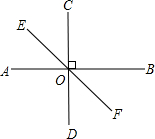 如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )
如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )
 如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )
如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )| A. | 30° | B. | 40° | ||
| C. | 50° | D. | 以上结果均不正确 |
9.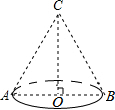 如图,将一个底面直径为12cm,高为8cm的圆锥形纸筒沿一条母线剪开,所得到的侧面展开图的面积为( )
如图,将一个底面直径为12cm,高为8cm的圆锥形纸筒沿一条母线剪开,所得到的侧面展开图的面积为( )
 如图,将一个底面直径为12cm,高为8cm的圆锥形纸筒沿一条母线剪开,所得到的侧面展开图的面积为( )
如图,将一个底面直径为12cm,高为8cm的圆锥形纸筒沿一条母线剪开,所得到的侧面展开图的面积为( )| A. | 30cm2 | B. | 30πcm2 | C. | 60πcm2 | D. | 120cm2 |
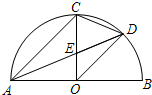 如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连结CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③△ODE∽△ADO;④CD2=CE•CO.其中正确结论的序号是①④.
如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,连结CD、OD,给出以下四个结论:①AC∥OD;②CE=OE;③△ODE∽△ADO;④CD2=CE•CO.其中正确结论的序号是①④.



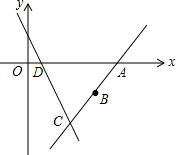 如图,已知点A(4,0)、点B(3,-$\frac{3}{2}$).y=-3x+3的图象交x轴于点D,直线AB与y=-3x+3的图象交于点C.
如图,已知点A(4,0)、点B(3,-$\frac{3}{2}$).y=-3x+3的图象交x轴于点D,直线AB与y=-3x+3的图象交于点C.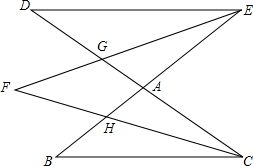 如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论.
如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论.