题目内容
1.在直角三角形ABC中,∠C=90°,$cosA=\frac{{\sqrt{3}}}{2}$,∠B的平分线BD交AC于D,BD=16.求AB的长.分析 首先根据锐角三角形函数值的知识求出∠B的度数,进而求出BC的长度,在直角三角形中,利用30°的角所对的直角边等于斜边的一半求出AB的长.
解答 解:在直角三角形ABC中,∠C=90°,
∵cosA=$\frac{{\sqrt{3}}}{2}$,
∴∠A=30°,
∴∠B=60°,
∵BD是∠B的平分线,
∴∠DBC=30°,
在直角三角形DBC中
cos30°=$\frac{BC}{BD}$,
∴BC=$16×\frac{{\sqrt{3}}}{2}=8\sqrt{3}$,
在直角三角形ACB中,
∵∠A=30°,
∴30°的角所对的直角边等于斜边的一半,
∴AB=$16\sqrt{3}$.
点评 本题主要考查了解直角三角形的知识,解答本题的关键是掌握锐角三角形函数的定义以及含30°角直角三角形的性质,此题难度不大.

练习册系列答案
相关题目
11.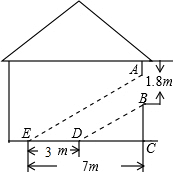 如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
 如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )| A. | 2m | B. | 2.4m | C. | 2.8m | D. | 3m |
12.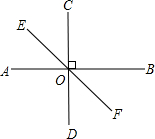 如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )
如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )
 如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )
如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )| A. | 30° | B. | 40° | ||
| C. | 50° | D. | 以上结果均不正确 |
9.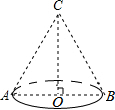 如图,将一个底面直径为12cm,高为8cm的圆锥形纸筒沿一条母线剪开,所得到的侧面展开图的面积为( )
如图,将一个底面直径为12cm,高为8cm的圆锥形纸筒沿一条母线剪开,所得到的侧面展开图的面积为( )
 如图,将一个底面直径为12cm,高为8cm的圆锥形纸筒沿一条母线剪开,所得到的侧面展开图的面积为( )
如图,将一个底面直径为12cm,高为8cm的圆锥形纸筒沿一条母线剪开,所得到的侧面展开图的面积为( )| A. | 30cm2 | B. | 30πcm2 | C. | 60πcm2 | D. | 120cm2 |
6.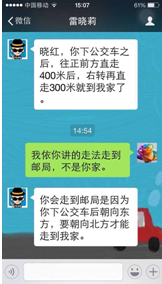 如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )
如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )
 如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )
如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )| A. | 向北直走700米,再向西直走100米 | B. | 向北直走100米,再向东直走700米 | ||
| C. | 向北直走300米,再向西直走400米 | D. | 向北直走400米,再向东直走300米 |
 如图,在△ABC中,AD是BC边上的中线,E、F是AC边的三等分点,连接BE交AD于G,连接DF,求AG:AD的值.
如图,在△ABC中,AD是BC边上的中线,E、F是AC边的三等分点,连接BE交AD于G,连接DF,求AG:AD的值.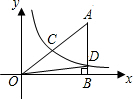 在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象经过AO的中点C,且与AB交于点D,则tan∠DOB的值为$\frac{3}{16}$.
在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象经过AO的中点C,且与AB交于点D,则tan∠DOB的值为$\frac{3}{16}$.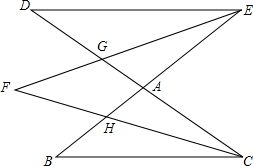 如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论.
如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论.