题目内容
3.(1)如图①所示,AB和DE是直立在地面上的两根木杆,BC是AB在太阳光下的影子,请你在图中画出此时木杆DE的影子(用线段EF表示).图②是直立在地面上的两根木杆及它们在灯光下的影子,请你在图中画出光源的位置(用点O表示);
(2)太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是20$\sqrt{3}$cm,请你求出皮球的半径.
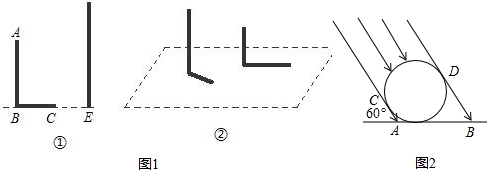
分析 (1)连接AC,作DF∥AC交直线BC于点F即可;分别作过两根木杆的顶端和相应的影子的顶端的直线得到的交点就是点光源所在处.
(2)根据题意建立直角三角形ABE,然后根据∠DBA=60°,AE=20$\sqrt{3}$可求出答案.
解答 解:(1)如图①所示:EF即为所求;
如图②所示:O即为所求;
(2)如图2,过点A作A⊥DB于点E,连接CD,
∵由题意得:DC=2R,AB=20$\sqrt{3}$,∠DBA=60°,
∴可得:DC=AE=ABsin60°=30(cm).
故皮球的半径为:15cm.
点评 本题考查平行投影的应用,属于基础题,解答本题的关键是建立直角三角形,然后利用三角函数值进行解答.

练习册系列答案
相关题目
11.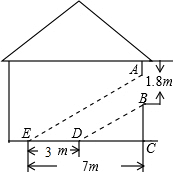 如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
 如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )| A. | 2m | B. | 2.4m | C. | 2.8m | D. | 3m |
18. 小丽想猜测学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为α,测倾器到旗杆底部的距离AD为a米,测倾器的高度AB为b米,那么旗杆的高度CD为( )
小丽想猜测学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为α,测倾器到旗杆底部的距离AD为a米,测倾器的高度AB为b米,那么旗杆的高度CD为( )
 小丽想猜测学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为α,测倾器到旗杆底部的距离AD为a米,测倾器的高度AB为b米,那么旗杆的高度CD为( )
小丽想猜测学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为α,测倾器到旗杆底部的距离AD为a米,测倾器的高度AB为b米,那么旗杆的高度CD为( )| A. | (atanα+b)米 | B. | (acosα+b)米 | C. | ($\frac{a}{tanα}$+b)米 | D. | ($\frac{a}{sinα}$+b)米 |
12.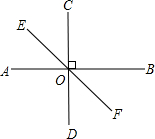 如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )
如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )
 如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )
如图,直线AB、EF相交于O点,CD⊥AB于O点,∠EOD=130°,则∠BOF的度数为( )| A. | 30° | B. | 40° | ||
| C. | 50° | D. | 以上结果均不正确 |





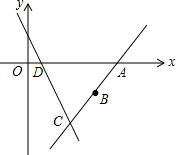 如图,已知点A(4,0)、点B(3,-$\frac{3}{2}$).y=-3x+3的图象交x轴于点D,直线AB与y=-3x+3的图象交于点C.
如图,已知点A(4,0)、点B(3,-$\frac{3}{2}$).y=-3x+3的图象交x轴于点D,直线AB与y=-3x+3的图象交于点C.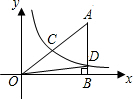 在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象经过AO的中点C,且与AB交于点D,则tan∠DOB的值为$\frac{3}{16}$.
在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=$\frac{3}{5}$,反比例函数y=$\frac{k}{x}$(k>0)的图象经过AO的中点C,且与AB交于点D,则tan∠DOB的值为$\frac{3}{16}$.