题目内容
6.一个正方形的边长是12cm、若从中挖去一个长为2xcm、宽为(x+1)cm的小长方形,剩余部分的面积为ycm2(1)写出y与x之间的函数解析式,并指出y是x的什么函数;
(2)当x的值为2时,剩余部分的面积是多少?
(3)当剩余部分的面积是104cm2时.相应的小长方形的长是多少?
分析 (1)根据矩形的面积公式列出函数表达式,判断函数类型;
(2)把x=2代入函数表达式,求出y的值即可;
(3)把y=104代入函数表达式,解方程即可.
解答 解:(1)y=122-2x(x+1)=-2x2-2x+144,此函数为二次函数;
(2)当x=2时,y=-2×4-2×2+144=132,
∴当x的值为2时,剩余部分的面积是132cm2;
(3)把y=104代入函数表达式,得
-2x2-2x+144=104
解得:x1=-5(不合题意,舍去),x2=4,
故当剩余部分的面积是104cm2时.相应的小长方形的长是8cm.
点评 本题主要考查的是二次函数的应用,根据题意列出函数关系式是解题的关键.

练习册系列答案
相关题目
17.某油库原来没有积存汽油,若以每小时进油1000千克的速度灌油3小时后,又以每小时1500千克的速度输出汽油,且油库存油量Q(千克)是时间t(时)的函数,则这个函数的大致图象是( )
| A. | 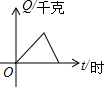 | B. | 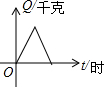 | C. | 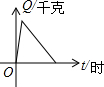 | D. | 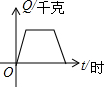 |
11.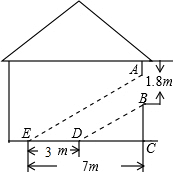 如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
 如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )
如图,阳光通过窗口照到室内,在地上留下3m宽的亮区,已知亮区一边到窗下的墙角的距离CE=7m,窗口高AB=1.8m,那么窗口底边离地面的高BC等于( )| A. | 2m | B. | 2.4m | C. | 2.8m | D. | 3m |
18. 小丽想猜测学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为α,测倾器到旗杆底部的距离AD为a米,测倾器的高度AB为b米,那么旗杆的高度CD为( )
小丽想猜测学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为α,测倾器到旗杆底部的距离AD为a米,测倾器的高度AB为b米,那么旗杆的高度CD为( )
 小丽想猜测学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为α,测倾器到旗杆底部的距离AD为a米,测倾器的高度AB为b米,那么旗杆的高度CD为( )
小丽想猜测学校旗杆的高度,她在地面A点安置测倾器,测得旗杆顶端C的仰角为α,测倾器到旗杆底部的距离AD为a米,测倾器的高度AB为b米,那么旗杆的高度CD为( )| A. | (atanα+b)米 | B. | (acosα+b)米 | C. | ($\frac{a}{tanα}$+b)米 | D. | ($\frac{a}{sinα}$+b)米 |
 如图,已知∠AOB.
如图,已知∠AOB.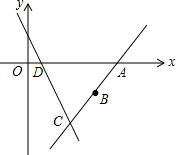 如图,已知点A(4,0)、点B(3,-$\frac{3}{2}$).y=-3x+3的图象交x轴于点D,直线AB与y=-3x+3的图象交于点C.
如图,已知点A(4,0)、点B(3,-$\frac{3}{2}$).y=-3x+3的图象交x轴于点D,直线AB与y=-3x+3的图象交于点C. 如图,在△ABC中,AD是BC边上的中线,E、F是AC边的三等分点,连接BE交AD于G,连接DF,求AG:AD的值.
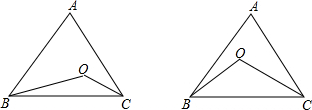
如图,在△ABC中,AD是BC边上的中线,E、F是AC边的三等分点,连接BE交AD于G,连接DF,求AG:AD的值.