题目内容
9. 2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 27~30 | 21 | 0.35 |
| B | 23~26 | m | x |
| C | 19~22 | n | y |
| D | 18及18以下 | 3 | 0.05 |
| 合计 | 60 | 1.00 |
(1)m=24,n=12,x=0.4,y=0.2;
(2)在扇形图中,B等级所对应的圆心角是144度;
(3)请你估计邯郸市这12万名初三毕业生成绩等级达到优秀和良好的大约有多少人?
(4)初三(1)班的甲、乙、丙、丁四人的成绩均为A,现决定从这四名同学中选两名参加学校组织的体育活动,直接写出恰好选中甲、乙两位同学的概率.
分析 (1)让总人数60乘以相应的百分比40%可得m的值,让总人数50减去其余已知人数可得n的值,x为相应百分比,将n的值除以50即为y的值;
(2)让360乘以相应频率即为B等级所对应的圆心角;
(3)该市初三毕业生总人数12万人乘以A、B两个等级的百分比的和即为所求的人数;
(4)列出从甲、乙、丙、丁四人选两人的6种结果,选中甲、乙两位同学的结果只有1种,由概率公式可得.
解答 解:(1)m=60×40%=24,n=60-21-24-3=12,x=40%=0.4,y=12÷60=0.2;
(2)40%×360°=144°;
(3)由上表可知达到优秀和良好的共有21+24=45人,12×$\frac{45}{60}$=9(万人),
答:估计邯郸市这12万名初三毕业生成绩等级达到优秀和良好的大约有9万人;
(4)∵从甲、乙、丙、丁四人选两人有如下6种结果:
(甲,乙)、(甲,丙)、(甲,丁)、(乙,丙)、(乙,丁)、(丙,丁),
恰好选中甲、乙两位同学的结果只有1种,
∴恰好选中甲、乙两位同学的概率为$\frac{1}{6}$;
故答案为:(1)24,12,0.4,0.2;(2)144.
点评 本题考查了频率分布直方图、用样本估计总体、扇形统计图、概率公式,读图时要全面细致,同时,解题方法要灵活多样,切忌死记硬背,要充分运用数形结合思想来解决由统计图形式给出的数学实际问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.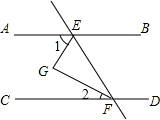 如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )
如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )
 如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )
如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )| A. | 40° | B. | 35° | C. | 25° | D. | 20° |
 尺规作图:已知⊙O及⊙O上一点A,如图.
尺规作图:已知⊙O及⊙O上一点A,如图.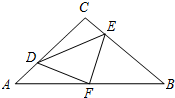 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论:
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF.在此运动变化的过程中,下列结论: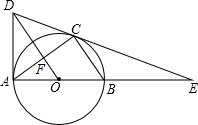 如图,AB为⊙O的直径,点C在⊙O上,连接BC、AC,作OD∥BC,与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,AB为⊙O的直径,点C在⊙O上,连接BC、AC,作OD∥BC,与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.