题目内容
14.计算:$|{-3}|+{(\frac{1}{3})^{-1}}-{(π-1)^0}+\sqrt{4}$.分析 原式利用零指数幂、负整数指数幂法则,绝对值的代数意义,以及算术平方根定义计算即可得到结果.
解答 解:原式=3+3-1+2=7.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
4.下列各数中是无理数的是( )
| A. | $\frac{10}{3}$ | B. | 3.1415 | C. | $\root{3}{8}$ | D. | $\sqrt{2}$ |
9. 2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
请你根据以上图表提供的信息,解答下列问题:
(1)m=24,n=12,x=0.4,y=0.2;
(2)在扇形图中,B等级所对应的圆心角是144度;
(3)请你估计邯郸市这12万名初三毕业生成绩等级达到优秀和良好的大约有多少人?
(4)初三(1)班的甲、乙、丙、丁四人的成绩均为A,现决定从这四名同学中选两名参加学校组织的体育活动,直接写出恰好选中甲、乙两位同学的概率.
 2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
2016年4月15日至5月15日,邯郸市约12万名初三毕业生参加了中考体育测试,为了了解今年初三毕业学生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 27~30 | 21 | 0.35 |
| B | 23~26 | m | x |
| C | 19~22 | n | y |
| D | 18及18以下 | 3 | 0.05 |
| 合计 | 60 | 1.00 |
(1)m=24,n=12,x=0.4,y=0.2;
(2)在扇形图中,B等级所对应的圆心角是144度;
(3)请你估计邯郸市这12万名初三毕业生成绩等级达到优秀和良好的大约有多少人?
(4)初三(1)班的甲、乙、丙、丁四人的成绩均为A,现决定从这四名同学中选两名参加学校组织的体育活动,直接写出恰好选中甲、乙两位同学的概率.
19.本学期的四次数学单元练习中,甲、乙两位同学的平均成绩一样,方差分别为1.0,0.6,由此可知( )
| A. | 甲比乙的成绩稳定 | B. | 甲乙两人的成绩一样稳定 | ||
| C. | 乙比甲的成绩稳定 | D. | 无法确定谁的成绩更稳定 |
6.甲、乙两地5月下旬的日平均气温统计如表(单位:℃):
则甲、乙两地这10天日平均气温的方差大小关系为:S甲2>S乙2.(填“>”、“<”或“=”)
| 甲地气温 | 24 | 30 | 28 | 24 | 22 | 26 | 27 | 26 | 29 | 24 |
| 乙地气温 | 24 | 26 | 25 | 26 | 24 | 27 | 28 | 26 | 28 | 26 |
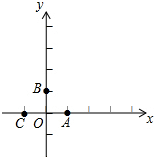 如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P7的坐标是(2,0),点P2016的坐标为(0,0).
如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(-1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1.使得点P1与点O关于点A成中心对称;第二次跳跃到点P2,使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3,使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4,使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5,使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P7的坐标是(2,0),点P2016的坐标为(0,0).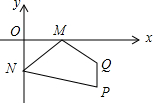 如图,点P的坐标是(3,-2),点Q的坐标是(3,-1),点M是x轴上一个动点,点N是y轴上的一个动点,则四边形MNPQ周长的最小值是2$\sqrt{13}$+1.
如图,点P的坐标是(3,-2),点Q的坐标是(3,-1),点M是x轴上一个动点,点N是y轴上的一个动点,则四边形MNPQ周长的最小值是2$\sqrt{13}$+1.