题目内容
18.问题情境:数学活动课上,老师出示了一个问题:如图(1),将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合,转动△DEF使DF⊥AB交AC于点G,DE交BC于点H.求两三角形重叠部分(四边形DHCG)的面积.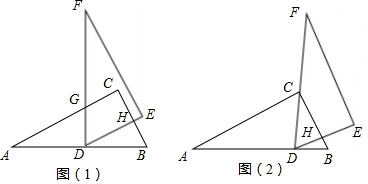
(1)独立思考:请解答老师提出的问题.
(2)合作交流:将△DEF绕点D继续旋转,如图(2),使DF经过点C,DE交BC于点H,你能求出两三角形重叠部分(△DHC)的面积,请写出解答过程.
(3)拓展探究:边EF在绕点D旋转的过程中扫过了一个圆环(注:填图形名称),该图形的面积为64π.
分析 (1)根据全等三角形的性质得到∠EDF=∠B,根据勾股定理得到AB=DF=10,根据三角形的中位线的性质得到DH=$\frac{1}{2}$AC=4,BH=CH=$\frac{1}{2}$BC=3,根据相似三角形的性质得到AG=$\frac{25}{4}$,CG=$\frac{7}{4}$,根据梯形的面积公式得到结论;
(2)如图(2),根据直角三角形的性质得到AD=BD=CD,由等腰三角形的性质得到∠ACD=∠A,根据余角的性质得到∠BCD=∠B,过H作HM⊥CD于M,由等腰三角形的性质得到DM=CM=$\frac{1}{2}$CD=$\frac{5}{2}$,根据相似三角形的性质得到DM=$\frac{10}{3}$,根据三角形的面积公式即可得到结论;
(3)边EF在绕点D旋转的过程中扫过了一个圆环,根据圆的面积公式得到结果.
解答 解:(1)在△ABC与△DEF中,$\left\{\begin{array}{l}{BC=DE}\\{∠ACB=∠DEF}\\{AC=EF}\end{array}\right.$,
∴△ABC≌△DEF,
∴∠EDF=∠B,
∵∠ACB=∠E=90°,
∴AB=DF=10,
∵DF⊥AB,
∴∠EDF+∠BDE=90°,
∴∠BDE=∠A,
∴DH∥AC,
∵AD=BD,
∴DH=$\frac{1}{2}$AC=4,BH=CH=$\frac{1}{2}$BC=3,
∵∠ADG=∠C=90°,∠A=∠A,
∴△ADG∽△ABC,
∴$\frac{AG}{AB}=\frac{AD}{AC}$,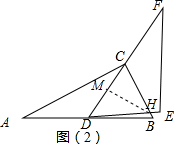
∴AG=$\frac{25}{4}$,
∴CG=$\frac{7}{4}$,
∴四边形DHCG的面积=$\frac{1}{2}$(4+$\frac{7}{4}$)×3=$\frac{69}{8}$,
(2)如图(2),
∵∠ACB=90°,D是AB的中点,
∴AD=BD=CD,
∴∠ACD=∠A,
∵∠A+∠B=∠ACD+∠BCD=90°,
∴∠BCD=∠B,
∵∠CDH=∠B,
∴∠CDH=∠DCH,
∴CH=DH,
过H作HM⊥CD于M,
则DM=CM=$\frac{1}{2}$CD=$\frac{5}{2}$,
∵∠HMD=∠ACB=90°,∠MDH=∠B,
∴△MDH∽△ABC,
∴$\frac{DM}{BC}=\frac{HM}{AC}$,即$\frac{\frac{5}{2}}{6}=\frac{MH}{8}$,
∴DM=$\frac{10}{3}$,
∴S△CDH=$\frac{1}{2}$×5×$\frac{10}{3}$=$\frac{25}{3}$;
(3)边EF在绕点D旋转的过程中扫过了一个圆环,
S圆环=102π-62π=64π,
故答案为:圆环,64π.
点评 本题考查了全等三角形的性质和判定、相似三角形的判定和性质、直角三角形斜边上的中线性质以及勾股定理和三角形面积和圆的面积的计算方法;本题难度较大,综合性强,培养学生综合运用定理进行推理论证和计算的能力.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | a6÷a3=a2 | B. | (a3)2=a5 | C. | (ab)3=ab3 | D. | a•a2=a3 |
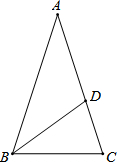 如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )
如图所示,已知在△ABC中,AB=AC,BC=BD,AD=DB,则∠A的度数是( )| A. | 30° | B. | 36° | C. | 45° | D. | 54° |