题目内容
13.用公式简便计算:(1)49$\frac{2}{3}$×50$\frac{1}{3}$
(2)1999×2001+1.
分析 (1)先变形,再根据平方差公式进行计算,即可求出答案;
(2)先变形,再根据平方差公式进行计算,即可求出答案.
解答 解:(1)原式=(50-$\frac{1}{2}$)×(50+$\frac{1}{2}$)
=502-($\frac{1}{2}$)2
=2500-$\frac{1}{4}$
=2499$\frac{3}{4}$;
(2)原式=(2000-1)×(2000+1)+1
=20002-12+1
=4000000.
点评 本题考查了平方差公式,能灵活运用公式进行计算是解此题的关键,注意:(a+b)(a-b)=a2-b2.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
1.已知反比例函数y=$\frac{2}{x}$,则在这个反比例函数图象上的点是( )
| A. | (-2,1) | B. | (1,2) | C. | (1,-2) | D. | (-2,-2) |
8.已知某种花粉的直径为0.000 000 000 254米,则0.000 000 000 254用科学记数法可表示为( )
| A. | 25.4×10-9 | B. | 2.54×10-10 | C. | 2.54×10-8 | D. | 2.54×109 |
 画出从正面、上面看到的几何体的形状图.
画出从正面、上面看到的几何体的形状图.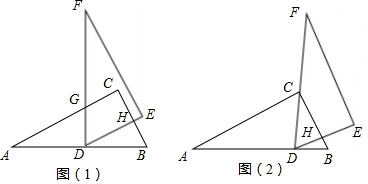
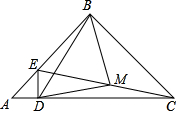 已知在△ABC中,∠ABC=90°,AB=BC=8cm,点D为AC一点,过点D作DE⊥AC交线段AB于点E,点M为EC的中点.
已知在△ABC中,∠ABC=90°,AB=BC=8cm,点D为AC一点,过点D作DE⊥AC交线段AB于点E,点M为EC的中点.