题目内容
11.解方程组和不等式(1)解方程组$\left\{\begin{array}{l}{x+2y=1}\\{3x-2y=11}\end{array}\right.$
(2)解不等式5x+15>4x+13并在数轴上表示它的解集.
分析 (1)①+②得出4x=12,求出x,把x的值代入①求出y即可;
(2)移项,合并同类项,求出不等式的解集,最后在数轴上表示出来即可.
解答 解:(1)$\left\{\begin{array}{l}{x+2y=1①}\\{3x-2y=11②}\end{array}\right.$
①+②得:4x=12,
解得:x=3,
把x=3代入①得:3+2y=1,
解得:y=-1,
所以原方程组的解为:$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$;
(2)5x+15>4x+13,
5x-4x>13-15,
x>-2,在数轴上表示为: .
.
点评 本题考查了解二元一次方程组,解一元一次不等式,在数轴上表示出不等式的解集的应用,能熟记知识点是解此题的关键.

练习册系列答案
相关题目
6.满足下列条件的三条线段a、b、c能构成三角形的是( )
| A. | a:b:c=1:2:3 | B. | a+b=4,a+b+c=9 | C. | a=3,b=4,c=5 | D. | a:b:c=1:1:2 |
3.有以下三个说法:①对顶角相等是真命题;②连接直线外一点与直线上个各点的所有线段中,垂线段最短;③平面直角坐标系内的所有点都分别属于四个象限;④经过一点有且只有一条直线与已知直线平行;其中错误的有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.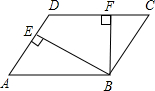 如图,在菱形ABCD中,BE⊥AD于E,BF⊥CD于F,且AE=DE,则∠EBF的度数是( )
如图,在菱形ABCD中,BE⊥AD于E,BF⊥CD于F,且AE=DE,则∠EBF的度数是( )
 如图,在菱形ABCD中,BE⊥AD于E,BF⊥CD于F,且AE=DE,则∠EBF的度数是( )
如图,在菱形ABCD中,BE⊥AD于E,BF⊥CD于F,且AE=DE,则∠EBF的度数是( )| A. | 75° | B. | 60° | C. | 50° | D. | 45° |
 如图,AB是⊙O的直径,AC是弦,OP⊥AC于点D,交⊙O于点E,连接BE、CE,∠P=∠BEC.
如图,AB是⊙O的直径,AC是弦,OP⊥AC于点D,交⊙O于点E,连接BE、CE,∠P=∠BEC.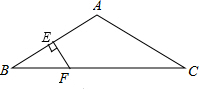 如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线EF交AB于E,交BC于F.求证:CF=2BF.
如图,△ABC中,AB=AC,∠A=120°,AB的垂直平分线EF交AB于E,交BC于F.求证:CF=2BF. 如图,在?ABCD中,AD=10,AC=8,BD=14,则△BOC的周长是21.
如图,在?ABCD中,AD=10,AC=8,BD=14,则△BOC的周长是21. 在?ABCD中,点E、F是对角线AC上两点,且AE=CF.
在?ABCD中,点E、F是对角线AC上两点,且AE=CF.