题目内容
3．
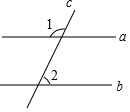如图，a∥b，∠2=62°，则∠1=（ ）| A． | 62° | B． | 128° | C． | 118° | D． | 28° |
分析 由a∥b，∠2=62°，根据两直线平行，同位角相等，即可求得∠3的度数，又由邻补角的定义，即可求得∠1的度数．
解答 
解：∵a∥b，∠2=62°，
∴∠3=∠2=62°，
∵∠1+∠3=180°，
∴∠1=118°．
故选：C．
点评 此题考查了平行线的性质与邻补角的定义．解题的关键是注意掌握两直线平行，同位角相等定理的应用．
练习册系列答案
名校课堂系列答案
相关题目
如图，△ABC中，D是BC边上一点，E是AD的中点，过点A作BC的平行线交CE的延长线于F，且AF=BD，连结BF．
如图，二次函数y=（x+m）2+k的图象与x轴交于A、B两点，顶点M的坐标为（1，-4）．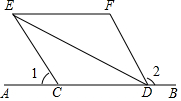
已知：如图，C、D是直线AB上两点，∠1+∠2=180°，DE平分∠CDF，EF∥AB．