题目内容
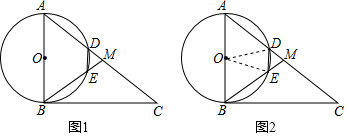
11.如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.(Ⅰ)求证:MD=ME;
(Ⅱ)如图2,连OD,OE,当∠C=30°时,求证:四边形ODME是菱形.
分析 (1)利用直角三角形斜边上的中线性质得MA=MB,则∠A=∠MBA,再利用圆内接四边形的性质证明∠MDE=∠MED,于是得到MD=ME;
(2)先证明△OAD和△OBE为等边三角形,再证明四边形DOEM为平行四边形,然后加上OD=OE可判断四边形ODME是菱形.
解答 解:(1)在Rt△ABC中,点M是AC的中点,
∴MA=MB,
∴∠A=∠MBA;
∵四边形ABED是圆内接四边形,
∴∠ADE+∠ABE=180°,
而∠ADE+∠MDE=180°,
∴∠MDE=∠MBA;
同理可得∠MED=∠A,
∴∠MDE=∠MED,
∴MD=ME;
(2)∵∠C=30°,
∴∠A=60°,
∴∠ABM=60°,
∴△OAD和△OBE为等边三角形,
∴∠BOE=60°,
∴∠BOE=∠A,
∴OE∥AC,
同理可得OD∥BM,
∴四边形DOEM为平行四边形,
而OD=OE,
∴四边形ODME是菱形.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了菱形的判定.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.已知多项式x-a与x2+2x-1的乘积中不含x2项,则常数a的值是( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
3.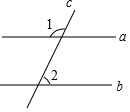 如图,a∥b,∠2=62°,则∠1=( )
如图,a∥b,∠2=62°,则∠1=( )
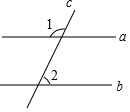 如图,a∥b,∠2=62°,则∠1=( )
如图,a∥b,∠2=62°,则∠1=( )| A. | 62° | B. | 128° | C. | 118° | D. | 28° |
1. 有这样一个问题:探究函数y=$\frac{1}{(x-2)^{2}}$的图象与性质,小静根据学习函数的经验,对函数y=$\frac{1}{(x-2)^{2}}$的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
有这样一个问题:探究函数y=$\frac{1}{(x-2)^{2}}$的图象与性质,小静根据学习函数的经验,对函数y=$\frac{1}{(x-2)^{2}}$的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
(1)函数y=$\frac{1}{(x-2)^{2}}$的自变量x的取值范围是x≠2;
(2)下表是y与x的几组对应值.
表中的m=4;
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
(4)结合函数图象,写出一条该函数图象的性质:函数图象关于直线x=2对称.
 有这样一个问题:探究函数y=$\frac{1}{(x-2)^{2}}$的图象与性质,小静根据学习函数的经验,对函数y=$\frac{1}{(x-2)^{2}}$的图象与性质进行了探究,下面是小静的探究过程,请补充完整:
有这样一个问题:探究函数y=$\frac{1}{(x-2)^{2}}$的图象与性质,小静根据学习函数的经验,对函数y=$\frac{1}{(x-2)^{2}}$的图象与性质进行了探究,下面是小静的探究过程,请补充完整:(1)函数y=$\frac{1}{(x-2)^{2}}$的自变量x的取值范围是x≠2;
(2)下表是y与x的几组对应值.
| x | … | -1 | 0 | 1 | $\frac{3}{2}$ | $\frac{5}{2}$ | 3 | 4 | … |
| y | … | $\frac{1}{9}$ | $\frac{1}{4}$ | 1 | 4 | m | 1 | $\frac{1}{4}$ | … |
(3)如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,根据描出的点画出该函数的图象;
(4)结合函数图象,写出一条该函数图象的性质:函数图象关于直线x=2对称.
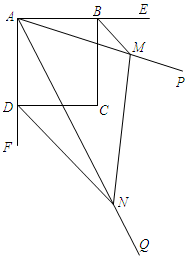 已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.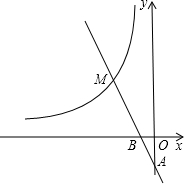 如图,反比例函数y=$\frac{k}{x}$的图象与过两点A(0,-2),B(-1,0)的一次函数的图象在第二象限内相交于点M(m,4).
如图,反比例函数y=$\frac{k}{x}$的图象与过两点A(0,-2),B(-1,0)的一次函数的图象在第二象限内相交于点M(m,4).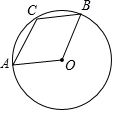 如图,OB为⊙O的半径,弦AC∥OB,∠A=50°,则∠B的度数为65°.
如图,OB为⊙O的半径,弦AC∥OB,∠A=50°,则∠B的度数为65°. 如图,在△ABC中,以AC为直径的⊙O分别交AB、BC于点D、E,连接DE,AD=BD,∠ADE=120°.
如图,在△ABC中,以AC为直径的⊙O分别交AB、BC于点D、E,连接DE,AD=BD,∠ADE=120°.