题目内容
13. 如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连结BF.
如图,△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连结BF.(1)求证:①△EAF≌△EDC;
②D是BC的中点;
(2)若AB=AC,求证:四边形AFBD是矩形.
分析 (1)①根据两直线平行,内错角相等求出∠AFE=∠DCE,然后利用“角角边”证明三角形全等即可;
②由全等三角形的性质容易得出结论;
(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形,再根据一个角是直角的平行四边形是矩形判定即可.
解答 (1)证明:①∵AF∥BC,
∴∠AFE=∠DCE,
∵点E为AD的中点,
∴AE=DE,
在△AEF和△EDC中,$\left\{\begin{array}{l}{∠AFE=∠DCE}&{\;}\\{∠AEF=∠DEC}&{\;}\\{AE=DE}&{\;}\end{array}\right.$,
∴△EAF≌△EDC(AAS);
②∵△AEF≌△DEC,
∴AF=CD,
∵AF=BD,
∴CD=BD;
即D是BC的中点;
(2)证明:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴平行四边形AFBD是矩形.
点评 本题考查了矩形的判定,全等三角形的判定与性质,平行四边形的判定,是基础题,明确有一个角是直角的平行四边形是矩形是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18. 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中①∠DCF=$\frac{1}{2}$∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.一定成立的是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中①∠DCF=$\frac{1}{2}$∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.一定成立的是( )
 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中①∠DCF=$\frac{1}{2}$∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.一定成立的是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中①∠DCF=$\frac{1}{2}$∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.一定成立的是( )| A. | ①② | B. | ①③④ | C. | ①②③ | D. | ①②④ |
5. 如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
 如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )| A. | 点B到直线l1的距离等于4 | B. | 点C到直线l1的距离等于5 | ||
| C. | 点C到AB的距离等于4 | D. | 点B到直线AC的距离等于5 |
3.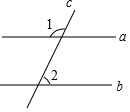 如图,a∥b,∠2=62°,则∠1=( )
如图,a∥b,∠2=62°,则∠1=( )
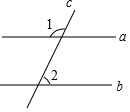 如图,a∥b,∠2=62°,则∠1=( )
如图,a∥b,∠2=62°,则∠1=( )| A. | 62° | B. | 128° | C. | 118° | D. | 28° |
 如图,AB∥CD,BC平分∠ACD,若∠1=54°,则∠2=63°.
如图,AB∥CD,BC平分∠ACD,若∠1=54°,则∠2=63°.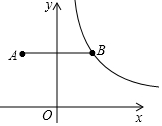 在平面直角坐标系中,点A(-2,3)关于y轴的对称点为点B,连接AB,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.
在平面直角坐标系中,点A(-2,3)关于y轴的对称点为点B,连接AB,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.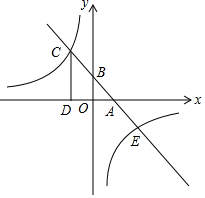 如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A,B 两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2$\sqrt{2}$,OA=OB=1.
如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A,B 两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2$\sqrt{2}$,OA=OB=1.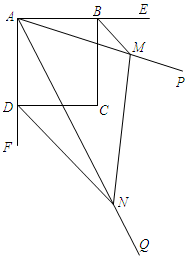 已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.