题目内容
18. 如图,二次函数y=(x+m)2+k的图象与x轴交于A、B两点,顶点M的坐标为(1,-4).
如图,二次函数y=(x+m)2+k的图象与x轴交于A、B两点,顶点M的坐标为(1,-4).(1)求A、B两点的坐标;
(2)设直线AM与y轴交于点C,求△BCM的面积;
(3)在抛物线上是否还存在点P,使得S△PMB=S△BCM?如果存在,求出点P的坐标;如果不存在,请说明理由.
分析 (1)所给二次函数解析式是顶点式,而顶点坐标是(1,-4),易求m、k的值,再把所求m、k的值代入二次函数中,令y=0,解关于x的一元二次方程,可求x=3或x=-1,进而可得A、B的坐标;
(2)首先求出直线AM的解析式,从而可得C点坐标(0,-2),利用S△BCM=S△ABM+S△ABC,进而可求其面积;
(3)根据同底等高的三角形面积相等,那么过点C作BM的平行线,观察可知与抛物线有2个交点,进而联立函数解析式得出答案.
解答 解:(1)根据题意,可得-m=1,k=-4,
解得:m=-1,k=-4,
把m=-1,k=-4代入函数解析式,得
y=(x-1)2-4,
令y=0,得(x-1)2-4=0,
解得:x=3或x=-1,
∴A点坐标是(-1,0),B点坐标是(3,0);
(2)如图所示:设AM所在直线解析式为:y=kx+b,
将A(-1,0),M(1,-4),代入可得:
$\left\{\begin{array}{l}{-k+b=0}\\{k+b=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=-2}\end{array}\right.$,
故AM所在直线解析式为:y=-2x-2,
令x=0,得y=-2,
∴点C的坐标是(0,-2),
∵B(3,0),C(0,-2),M(1,-4),
S△BCM=S△ABM+S△ABC=$\frac{1}{2}$×AB×4-$\frac{1}{2}$×AB×CO=8-4=4;
(3)如图所示:过点C作BM的平行线,此时直线BM与抛物线的交点即为P点坐标,
设BM所在直线解析式为:y=ax+c,将B,M分别代入函数解析式可得:
$\left\{\begin{array}{l}{a+c=-4}\\{3a+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{c=-6}\end{array}\right.$,
故BM所在直线解析式为:y=2x-6,
∵CN∥BM,
∴设直线CN的解析式为:y=2x+d,
将C点代入可得:y=2x-2,
故将y=2x-2与y=(x-1)2-4联立得:
$\left\{\begin{array}{l}{y=2x-2}\\{y=(x-1)^{2}-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=2-\sqrt{5}}\\{{y}_{1}=2-2\sqrt{5}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2+\sqrt{5}}\\{{y}_{2}=2+2\sqrt{5}}\end{array}\right.$,
故P点坐标为:(2-$\sqrt{5}$,2-2$\sqrt{5}$),(2+$\sqrt{5}$,2+2$\sqrt{5}$).
点评 本题考查了二次函数综合题以及待定系数法求一次函数解析式等知识,解题关键是注意掌握二次函数顶点式的表示方法以及求任意三角形面积时,同底等高的三角形面积相等.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案| A. |  | B. |  | C. | 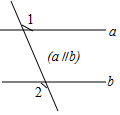 | D. |  |
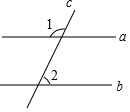 如图,a∥b,∠2=62°,则∠1=( )
如图,a∥b,∠2=62°,则∠1=( )| A. | 62° | B. | 128° | C. | 118° | D. | 28° |
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | $\sqrt{(-2)^{2}}$=2 | C. | $\sqrt{{6}^{2}}$=±6 | D. | $\sqrt{(-5)^{2}}$=±5 |
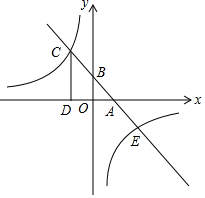 如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A,B 两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2$\sqrt{2}$,OA=OB=1.
如图,已知一次函数y=k1x+b的图象分别与x轴、y轴的正半轴交于 A,B 两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于 C,E 两点,点 C 在第二象限,过点 C 作CD⊥x轴于点 D,AC=2$\sqrt{2}$,OA=OB=1.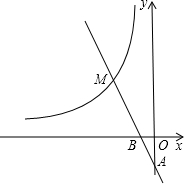 如图,反比例函数y=$\frac{k}{x}$的图象与过两点A(0,-2),B(-1,0)的一次函数的图象在第二象限内相交于点M(m,4).
如图,反比例函数y=$\frac{k}{x}$的图象与过两点A(0,-2),B(-1,0)的一次函数的图象在第二象限内相交于点M(m,4).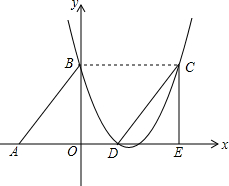 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过B点,且顶点在直线x=$\frac{5}{2}$上
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过B点,且顶点在直线x=$\frac{5}{2}$上