题目内容
6．计算：$\frac{5}{12}÷\frac{3}{4}÷\frac{1}{3}$．分析 把除法改为乘法，约分计算即可．
解答 解：$\frac{5}{12}÷\frac{3}{4}÷\frac{1}{3}$，
=$\frac{5}{12}×\frac{4}{3}×3$，
=$\frac{5}{3}$．
点评 本题主要考查的是有理数的除法，熟练掌握有理数的乘除法则是解题的关键．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
3．
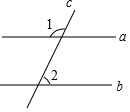如图，a∥b，∠2=62°，则∠1=（ ）
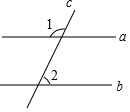如图，a∥b，∠2=62°，则∠1=（ ）| A． | 62° | B． | 128° | C． | 118° | D． | 28° |
4．
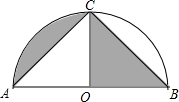如图，AB为半圆O的直径，C为$\widehat{AB}$的中点，若AB=2，则图中阴影部分的面积是（ ）
如图，AB为半圆O的直径，C为$\widehat{AB}$的中点，若AB=2，则图中阴影部分的面积是（ ）| A． | $\frac{π}{2}$ | B． | $\frac{1}{2}$+$\frac{π}{2}$ | C． | $\frac{π}{4}$ | D． | $\frac{1}{2}$+$\frac{π}{4}$ |
1．
有这样一个问题：探究函数y=$\frac{1}{（x-2）^{2}}$的图象与性质，小静根据学习函数的经验，对函数y=$\frac{1}{（x-2）^{2}}$的图象与性质进行了探究，下面是小静的探究过程，请补充完整：
（1）函数y=$\frac{1}{（x-2）^{2}}$的自变量x的取值范围是x≠2；
（2）下表是y与x的几组对应值．
表中的m=4；
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，根据描出的点画出该函数的图象；
（4）结合函数图象，写出一条该函数图象的性质：函数图象关于直线x=2对称．
有这样一个问题：探究函数y=$\frac{1}{（x-2）^{2}}$的图象与性质，小静根据学习函数的经验，对函数y=$\frac{1}{（x-2）^{2}}$的图象与性质进行了探究，下面是小静的探究过程，请补充完整：（1）函数y=$\frac{1}{（x-2）^{2}}$的自变量x的取值范围是x≠2；
（2）下表是y与x的几组对应值．
| x | … | -1 | 0 | 1 | $\frac{3}{2}$ | $\frac{5}{2}$ | 3 | 4 | … |
| y | … | $\frac{1}{9}$ | $\frac{1}{4}$ | 1 | 4 | m | 1 | $\frac{1}{4}$ | … |
（3）如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，根据描出的点画出该函数的图象；
（4）结合函数图象，写出一条该函数图象的性质：函数图象关于直线x=2对称．
如图，在Rt△ABC中，∠C=90°，AC=6，∠A的平分线交BC于点D，DE⊥AB于点E，且BE=4，求DE的长．