题目内容
14.在平面直角坐标系中画出直线y=$\frac{1}{3}$x+1的图象,并根据图象回答下列问题:(1)写出直线与x轴、y轴的交点的坐标;
(2)求出直线与坐标轴围成的三角形的面积;
(3)若直线y=kx+b与直线y=$\frac{1}{2}$x+1关于y轴对称,求k、b的值.
分析 (1)根据题意,分析可得在y=$\frac{1}{3}$x+1中,当x=-3时,y=0,x=0时,y=1,据此可以作出图象;
(2)根据三角形的面积公式计算即可.
(3)根据直线y=$\frac{1}{2}$x+1求得直线y=$\frac{1}{2}$x+1关于y轴的对称点,然后根据待定系数法求得即可.
解答 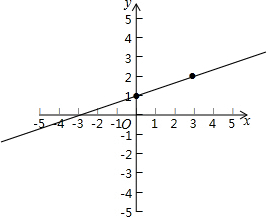 解:(1)令y=0得x=-3,令x=0得y=1,
解:(1)令y=0得x=-3,令x=0得y=1,
可得A点坐标为(-3,0),
B点坐标为(0,1)
画出图形如图:
(2)因为A(-3,0),B(0,1)
所以OA=3,OB=1,由三角形面积公式可知
S△AOB=$\frac{1}{2}$OA×OB=$\frac{1}{2}$×3×1=$\frac{3}{2}$;
(3)直线y=$\frac{1}{2}x$+1与x轴的交点为(-2,0),与y轴的交点为(0,1);
∴点(-2,0)关于y轴的对称点为(2,0),点(0,1)关于y轴的对称点为(0,1),
把点(2,0)、(0,1)代入y=kx+b得$\left\{\begin{array}{l}{2k+b=0}\\{b=1}\end{array}\right.$,
解得k=-$\frac{1}{2}$,b=1.
点评 本题主要考查一次函数图象以及待定系数法求一次函数的解析式,熟练掌握一次函数图象与性质是解题的关键.

练习册系列答案
相关题目
5. 如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
 如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
如图,点A在直线l1上,点B,C分别在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )| A. | 点B到直线l1的距离等于4 | B. | 点C到直线l1的距离等于5 | ||
| C. | 点C到AB的距离等于4 | D. | 点B到直线AC的距离等于5 |
19.已知多项式x-a与x2+2x-1的乘积中不含x2项,则常数a的值是( )
| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
3.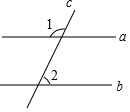 如图,a∥b,∠2=62°,则∠1=( )
如图,a∥b,∠2=62°,则∠1=( )
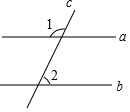 如图,a∥b,∠2=62°,则∠1=( )
如图,a∥b,∠2=62°,则∠1=( )| A. | 62° | B. | 128° | C. | 118° | D. | 28° |
4.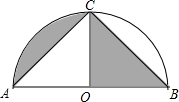 如图,AB为半圆O的直径,C为$\widehat{AB}$的中点,若AB=2,则图中阴影部分的面积是( )
如图,AB为半圆O的直径,C为$\widehat{AB}$的中点,若AB=2,则图中阴影部分的面积是( )
 如图,AB为半圆O的直径,C为$\widehat{AB}$的中点,若AB=2,则图中阴影部分的面积是( )
如图,AB为半圆O的直径,C为$\widehat{AB}$的中点,若AB=2,则图中阴影部分的面积是( )| A. | $\frac{π}{2}$ | B. | $\frac{1}{2}$+$\frac{π}{2}$ | C. | $\frac{π}{4}$ | D. | $\frac{1}{2}$+$\frac{π}{4}$ |
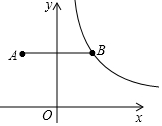 在平面直角坐标系中,点A(-2,3)关于y轴的对称点为点B,连接AB,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.
在平面直角坐标系中,点A(-2,3)关于y轴的对称点为点B,连接AB,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点.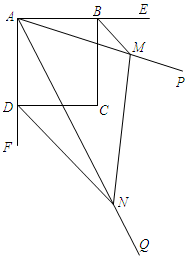 已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.
已知:如图,四边形ABCD是正方形,∠PAQ=45°,将∠PAQ绕着正方形的顶点A旋转,使它与正方形ABCD的两个外角∠EBC和∠FDC的平分线分别交于点M和N,连接MN.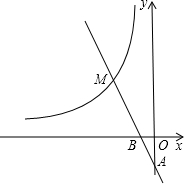 如图,反比例函数y=$\frac{k}{x}$的图象与过两点A(0,-2),B(-1,0)的一次函数的图象在第二象限内相交于点M(m,4).
如图,反比例函数y=$\frac{k}{x}$的图象与过两点A(0,-2),B(-1,0)的一次函数的图象在第二象限内相交于点M(m,4).