题目内容
4.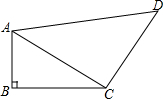 如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且AB⊥BC.求证AC⊥CD.
如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且AB⊥BC.求证AC⊥CD.
分析 在△ABC中,根据勾股定理求出AC2的值,再在△ACD中根据勾股定理的逆定理,判断出AC⊥CD.
解答 证明:在△ABC中AB⊥BC,根据勾股定理:AC2=AB2+BC2=12+22=5,
∵在△ACD中,AC2+CD2=5+4=9,AD2=9,
∴AC2+CD2=AD2,
∴根据勾股定理的逆定理,△ACD为直角三角形,
∴AC⊥CD.
点评 本题考查勾股定理与其逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
13.将抛物线y=5x2先向左平移2个单位,再向上平移3个单位后得到新的抛物线,则新抛物线的表达式是( )
| A. | y=5(x-2)2+3 | B. | y=5(x+2)2+3 | C. | y=5(x-2)2-3 | D. | y=5(x+2)2-3 |

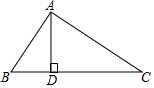 如图,∠BAC=∠ADB=90°,则下列结论
如图,∠BAC=∠ADB=90°,则下列结论