题目内容
19.完成下列解题过程.如图.己知CD垂直于AB,FG垂直于AB,∠1=∠2,求证:DE∥BC.

解:因为CD⊥AB,FG⊥FG(已知)
所以∠CDB=∠FGB=90°,
所以CD∥GF(两直线平行,同位角相等).
又因为∠1=∠2(已知),
所以∠2=∠DCB(等量代换)
所以DE∥BC(同位角相等,两直线平行)
分析 先根据垂直的性质得出∠CDB=∠FGB=90°,故可得出CD∥GF,再由∠1=∠2可得出∠2=∠DCB,据此可得出结论.
解答 解:∵CD⊥AB,FG⊥FG(已知),
∴∠CDB=∠FGB=90°,
∴CD∥GF(两直线平行,同位角相等).
又∵∠1=∠2(已知),
∴∠2=∠DCB(等量代换),
∴DE∥BC(同位角相等,两直线平行).
故答案为:CD∥GF,等量代换,同位角相等,两直线平行.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
相关题目
10.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  等边三角形 | B. |  平行四边形 | C. |  正六边形 | D. |  五角星 |
7.“关于x的函数y=(1-m)x2+2x+1的图象与x轴至少有一个交点”是真命题,则m的值不可以是( )
| A. | m=1 | B. | m=0 | C. | m=-1 | D. | m=2 |
8.下列图形中是轴对称图形,但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
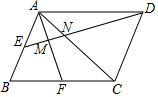 如图,点E,F分别是?ABCD两边AB、BC的中点,且AF、AC分别与ED交于M、N两点,有下列结论:①MN:ME=2:3;②MN:DN=1:4;③N是DE的三等分点;④△AMN~△DMA.其中正确的是:①③.(把所有正确结论的序号都选上)
如图,点E,F分别是?ABCD两边AB、BC的中点,且AF、AC分别与ED交于M、N两点,有下列结论:①MN:ME=2:3;②MN:DN=1:4;③N是DE的三等分点;④△AMN~△DMA.其中正确的是:①③.(把所有正确结论的序号都选上)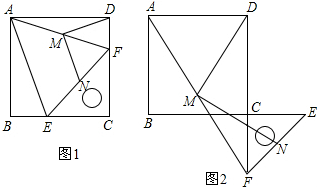
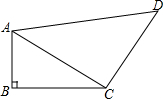 如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且AB⊥BC.求证AC⊥CD.
如图,在四边形ABCD中,AB=1,BC=2,CD=2,AD=3,且AB⊥BC.求证AC⊥CD.