题目内容
7. 已知△ABC为等边三角形,延长BC到M,CA到N,使CM=AN,连BN交MA的延长线于Q,求∠BQM.
已知△ABC为等边三角形,延长BC到M,CA到N,使CM=AN,连BN交MA的延长线于Q,求∠BQM.
分析 由△ABC为等边三角形,易得AB=BC,∠ABC=∠ACB=60°,又由BM=CN,即可证得△ABM≌△BCN,然后由全等三角形的对应角相等,求得答案.
解答 解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=60°,
在△ABM和△BCN中,
∵$\left\{\begin{array}{l}AB=BC\\∠ABM=∠ACB\\ BM=CN\end{array}\right.$,
∴△ABM≌△BCN(SAS),
∴∠BAM=∠CBN,
∴∠CBN+∠AMB=∠BAM+∠AMB=180°-∠ABC=120°,
∴∠BQM=180°-(∠CBN+∠AMB)=60°.
点评 此题考查了全等三角形的判定与性质以及等边三角形的性质.解题的关键是利用SAS证得△ABM≌△BCN.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
18.如图1,在四边形ABCD中,∠D=60°,点P,Q同时从点D出发,以每秒1个单位长度的速度分别沿D→A→B→C和D→C→B方向运动至相遇时停止,连接PQ.设点P运动的路程为x,PQ的长y,y与x之间满足的函数关系的图象如图2,则下列说法中不正确的是( )

| A. | AB∥CD | B. | AB=8 | ||
| C. | S四边形ABCD=$\frac{161\sqrt{3}}{4}$ | D. | ∠B=135° |
 如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,如果正方形ABCD的面积为64cm2,估计四边形EFGH的每条边的长.(精确到0.01cm)
如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,如果正方形ABCD的面积为64cm2,估计四边形EFGH的每条边的长.(精确到0.01cm)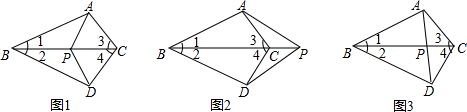
 如图,在△ABC中,AB=AC,BD=CD,则∠B=∠C,请说明理由.
如图,在△ABC中,AB=AC,BD=CD,则∠B=∠C,请说明理由. 如图,∠AOB=60°,其内部的点M到OA的距离MF=1,到OB的距离ME=2,求线段OM的长.
如图,∠AOB=60°,其内部的点M到OA的距离MF=1,到OB的距离ME=2,求线段OM的长.