题目内容
已知一个半圆的圆心O在坐标原点，直径在x轴上，且与y轴交于点（0，1），该半圆的任意一条半径与半圆交于点P，过P作PN垂直于x轴，N为垂足，则∠OPN的平分线一定经过点（ ）
| A、（1，0） | ||
| B、（-1，0） | ||
C、（0，-
| ||
| D、（0，-1） |
考点：垂径定理,坐标与图形性质
专题：计算题
分析：如图，设∠OPN的角平分线与y轴交于M点，PM是角平分线，所以∠1=∠2，PN垂直于x轴，所以，PN平行于y轴，所以∠1=∠3，所以∠2=∠3，所以OP=OM，即OM等于半径，所以M点坐标为（0，-1）．
解答：
解：如图，
设∠OPN的角平分线与y轴交于M点，
∵PM是角平分线，∴∠1=∠2，
∵PN⊥x轴，∴PN∥y轴，
∴∠1=∠3，
∴∠2=∠3，
∴OP=OM，即OM等于半径，
∴M点坐标为（0，-1）．
故选D．
解：如图，设∠OPN的角平分线与y轴交于M点，
∵PM是角平分线，∴∠1=∠2，
∵PN⊥x轴，∴PN∥y轴，
∴∠1=∠3，
∴∠2=∠3，
∴OP=OM，即OM等于半径，
∴M点坐标为（0，-1）．
故选D．
点评：本题考查了垂径定理与坐标与图形的性质，以及角平分线的性质，是基础知识要熟练掌握．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
用长度为2l的材料围成一个矩形场地，中间有2个隔墙，要使矩形的面积最大，则隔墙的长度为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、l |
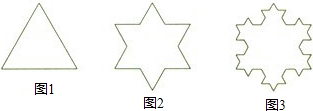
我们来探究“雪花曲线”的有关问题：如图1是长为1的正三角形，现将它作如下变换：取三角形各边的三等分点向形外作没有底边的等边三角形，这样得到一个六角星（如图2）；继续对六角星各边施行相同的变换，得到“雪花形”（如图3）．如此继续下去，第4次变换后得到的图形的周长应等于（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设S=
+
+…+
+
，则与S最接近的整数是（ ）
1+
|
1+
|
1+
|
1+
|
| A、2005 | B、2006 |
| C、2007 | D、2008 |
已知|x|=3x+1，则（64x2+48x+9）2005=（ ）
| A、0 | B、1 | C、-1 | D、无法计算 |