题目内容
有5家合用一口井,各家准备提水用的绳子都不一样长,而且都太短.井的深度等于A家绳长的2倍加上B家的绳长,或等于B家绳长的3倍加上C家的绳长,或等于C家绳长的4倍加上D家的绳长,或等于D家绳长的5倍加上E家的绳长,或等于E家绳长的6倍加上A家的绳长.问井深多少?各家的绳长各是多少?
考点:应用类问题
专题:计算题
分析:设井的深度是x,五户绳长依次是a,b,c,d,e.列出方程组,得出不定方程组,把e看成已知数,求出其余各个数即可.
解答:解:设井的深度是x,五户绳长以此是a,b,c,d,e,由题意,得.
,
∵方程组有方程5个,而6个未知数,
∴方程组是不定方程组,有无数组解,
我们把e看成已知数,用e把各个数表示出来,
由(3)-(4),得
d=
(6),
由(5)-(2),得
b=
(7),
把(6)、(7)代入原方程组,得
a=
e
b=
e,
c=
e,
d=
e,
把b和d代入以上方程组求出成方程组解得x=
e,
e取一个符合条件的任意一个数,就对应一组解,
故井深是
e米.
|
∵方程组有方程5个,而6个未知数,
∴方程组是不定方程组,有无数组解,
我们把e看成已知数,用e把各个数表示出来,
由(3)-(4),得
d=
| 4c-e |
| 4 |
由(5)-(2),得
b=
| 6e+a-c |
| 3 |
把(6)、(7)代入原方程组,得
a=
| 265 |
| 76 |
b=
| 191 |
| 76 |
c=
| 37 |
| 19 |
d=
| 129 |
| 76 |
把b和d代入以上方程组求出成方程组解得x=
| 721 |
| 76 |
e取一个符合条件的任意一个数,就对应一组解,
故井深是
| 721 |
| 76 |
点评:本题主要考查应用类问题的知识点,理解题意能力,关键是由方程表示数量关系得出方程组,难点是选择适当的方法消去多个未知数求解.

练习册系列答案
相关题目
 已知抛物线y=ax2+bx+c如图所示,则下列结论中,正确的是( )
已知抛物线y=ax2+bx+c如图所示,则下列结论中,正确的是( )| A、a>0 |
| B、a-b+c>0 |
| C、b2-4ac<0 |
| D、2a+b=0 |
设n,k为正整数,A1=
,A2=
,A3=
…Ak=
,已知A100=2005,则n=( )
| (n+3)(n-1)+4 |
| (n+5)A1+4 |
| (n+7)A2+4 |
| (n+2k+1)Ak-1+4 |
| A、1806 | B、2005 |
| C、3612 | D、4011 |
已知一个半圆的圆心O在坐标原点,直径在x轴上,且与y轴交于点(0,1),该半圆的任意一条半径与半圆交于点P,过P作PN垂直于x轴,N为垂足,则∠OPN的平分线一定经过点( )
| A、(1,0) | ||
| B、(-1,0) | ||
C、(0,-
| ||
| D、(0,-1) |
 如图,已知AB是⊙O的直径,弦CD⊥AB于H,AC=10,CD=12,那么sin∠ABD的值是
如图,已知AB是⊙O的直径,弦CD⊥AB于H,AC=10,CD=12,那么sin∠ABD的值是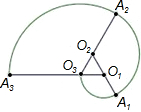 如图,一条螺旋线按以下方式生成:△O1O2O3为等边三角形,边长为1,曲线O3A1,A1A2,A2A3分别以O1,O2,O3为圆心,O1O3,O2A1,O3A2为半径的圆弧,曲线O3A1A2A3称为螺旋线O1旋转一圈,以后又以O1为圆心,O1O3为半径画圆弧,交O2O1得延长线于A4,…,等等,假设此螺旋线共绕O1旋转2圈,则此螺旋线的长度与圆周率π的比值为
如图,一条螺旋线按以下方式生成:△O1O2O3为等边三角形,边长为1,曲线O3A1,A1A2,A2A3分别以O1,O2,O3为圆心,O1O3,O2A1,O3A2为半径的圆弧,曲线O3A1A2A3称为螺旋线O1旋转一圈,以后又以O1为圆心,O1O3为半径画圆弧,交O2O1得延长线于A4,…,等等,假设此螺旋线共绕O1旋转2圈,则此螺旋线的长度与圆周率π的比值为