题目内容

线段AB被分为2：3：4三部分，已知第一部分和第三部分的中点间的距离是5.4cm，则线段AB的长度应为
 
．
考点：两点间的距离
专题：
分析：根据题意，画出图形，根据AC：CD：BD=2：3：4可设AC=2x，则CD=3c，BD=4x，点M是AC的中点，点N是BD的中点，则CM=
1
2
AC、DN=
1
2
BD，故MN=CM+CD+DN，从而得到x的值，进而可得出结论．
解答：解：如图，AC：CD：BD=2：3：4，设AC=2x，则CD=3c，BD=4x，
∵点M是AC的中点，点N是BD的中点
∴CM=
1
2
AC=x，DN=
1
2
BD=2x
∴MN=CM+CD+DN=6x=5.4，解得x=0.9
∴AB=2x+3x+4x=9x=9×0.9=8.1（cm）．
故答案为：8.1cm．
点评：本题考查的是两点间的距离，熟知各线段之间的和、差及倍数关系是解答此题的关键．
练习册系列答案
相关题目
已知圆锥的底面积为25π，母线长为13cm，这个圆锥的高为
 
，侧面积为
 
．
观察下列算式：
1
1×2
=1-
1
2
，
1
2×3
=
1
2
-
1
3
，
1
3×4
=
1
3
-
1
4
，
将以上三个式子两边分别相加，得
1
1×2
+
1
2×3
+
1
3×4
=1-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
=1-
1
4
=
3
4
，
（1）猜想：
1
n(n+1)
=
 
；
（2）直接写出下列各式的结果：
①已知|ab-2|+|a-1|=0，则
1
ab
+
1
(a+1)(b+1)
+
1
(a+2)(b+2)
+…
1
(a+2014)(b+2014)
=
 
；
②
1
100×101
+
1
101×102
+…+
1
n(n+1)
=
 
；
（3）探究并计算：
1
2×4
+
1
4×6
+
1
6×8
+…+
1
2012×2014
．
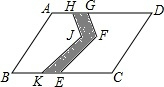如图，在平行四边形ABCD这块土地上，有一条小路（阴影部分），现要把它改为经过点E的直路，并保持小路两侧土地的面积不变，请在图中画出你设计的小路，并说明理由．
已知，如图，AB为⊙O的直径，E为⊙O外一点，EB，EC分别切⊙O于点B，C，求证：AC∥OE．
在平面直角坐标系中，已知点A（-4，0），B（2，0），若点C在一次函数y=-
1
2
x+2的图象上，且△ABC为直角三角形，求出点C的坐标．
已知一个圆柱的面积是168π，高为8，求该圆柱的底面直径．
已知方程（a-x）2-4（b-x）（c-x）=0，试说明：
（1）此方程必有实数根；
（2）若a、b、c为△ABC的三边长，方程有两个相等的实数根，则△ABC为等边三角形．
k取哪些值时，方程
2
3
x-3k=5（x-k）+1的解是非正数？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网