题目内容
观察下列算式:
=1-
,
=
-
,
=
-
,
将以上三个式子两边分别相加,得
+
+
=1-
+
-
+
-
=1-
=
,
(1)猜想:
= ;
(2)直接写出下列各式的结果:
①已知|ab-2|+|a-1|=0,则
+
+
+…
= ;
②
+
+…+
= ;
(3)探究并计算:
+
+
+…+
.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
将以上三个式子两边分别相加,得
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
(1)猜想:
| 1 |
| n(n+1) |
(2)直接写出下列各式的结果:
①已知|ab-2|+|a-1|=0,则
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2014)(b+2014) |
②
| 1 |
| 100×101 |
| 1 |
| 101×102 |
| 1 |
| n(n+1) |
(3)探究并计算:
| 1 |
| 2×4 |
| 1 |
| 4×6 |
| 1 |
| 6×8 |
| 1 |
| 2012×2014 |
考点:分式的加减法,有理数的混合运算
专题:规律型
分析:(1)观察已知等式,猜想得到结果即可;
(2)①利用非负数的性质求出a与b的值,代入原式后利用拆项法变形,计算即可得到结果;
②原式利用拆项法变形后,计算即可得到结果;
(3)原式利用拆项法变形后,计算即可得到结果.
(2)①利用非负数的性质求出a与b的值,代入原式后利用拆项法变形,计算即可得到结果;
②原式利用拆项法变形后,计算即可得到结果;
(3)原式利用拆项法变形后,计算即可得到结果.
解答:解:(1)
=
-
;
(2)①∵|ab-2|+|a-1|=0,
∴a=1,b=2,
则原式=
+
+…+
=1-
+
-
+…+
-
=1-
=
;
②原式=
-
+
-
+…+
-
=
-
=
;
(3)原式=
(
-
+
-
+…+
-
)=
(
-
)=
.
故答案为:(1)
-
;(2)①
;②
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(2)①∵|ab-2|+|a-1|=0,
∴a=1,b=2,
则原式=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2015×2016 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2015 |
| 1 |
| 2016 |
| 1 |
| 2016 |
| 2015 |
| 2016 |
②原式=
| 1 |
| 100 |
| 1 |
| 101 |
| 1 |
| 101 |
| 1 |
| 102 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 100 |
| 1 |
| n+1 |
| n-99 |
| 100(n+1) |
(3)原式=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2012 |
| 1 |
| 2014 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2014 |
| 1021 |
| 4028 |
故答案为:(1)
| 1 |
| n |
| 1 |
| n+1 |
| 2015 |
| 2016 |
| n-99 |
| 100(n+1) |
点评:此题考查了分式的加减法,以及有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 如图,OA是⊙O的半径,以OA为直径作⊙O′,⊙O的半径OC交⊙O′于点B,则
如图,OA是⊙O的半径,以OA为直径作⊙O′,⊙O的半径OC交⊙O′于点B,则 |
| AC |
 |
| AB |
| A、两弧所含的度数相等 |
| B、两弧是等弧 |
| C、两弧的长度相等 |
| D、弧AC的长度大 |
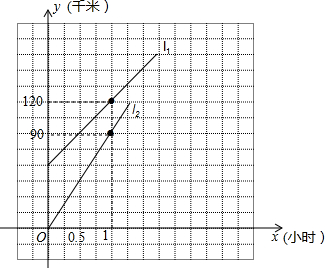 王经理从办公室乘A车去某市参加会议,开车50分钟后,发现有一重要文件遗漏在办公室中,他立即打电话通知秘书,让他拿着文件开车送往开会地点,10分钟后秘书乘B车开始按王经理乘车路线追赶,如图所示的l1和l2表示A、B两车相对于出发地的距离y(千米)与追赶时间x(小时)之间的关系:
王经理从办公室乘A车去某市参加会议,开车50分钟后,发现有一重要文件遗漏在办公室中,他立即打电话通知秘书,让他拿着文件开车送往开会地点,10分钟后秘书乘B车开始按王经理乘车路线追赶,如图所示的l1和l2表示A、B两车相对于出发地的距离y(千米)与追赶时间x(小时)之间的关系: 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,以直角顶点C为旋转中心,将△ABC逆时针旋转到△A′B′C的位置,其中A′,B′分别是A,B的对应点,当点B′,C,A在一条直线上时,∠A′BA的度数为( )
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,以直角顶点C为旋转中心,将△ABC逆时针旋转到△A′B′C的位置,其中A′,B′分别是A,B的对应点,当点B′,C,A在一条直线上时,∠A′BA的度数为( )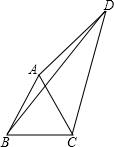 在四边形ABCD中,△ABC是等边三角形,∠ADC=30°,AD=3,BD=2
在四边形ABCD中,△ABC是等边三角形,∠ADC=30°,AD=3,BD=2