题目内容
已知圆锥的底面积为25π,母线长为13cm,这个圆锥的高为 ,侧面积为 .
考点:圆锥的计算
专题:计算题
分析:设圆锥的底面圆的半径为r,根据圆的面积公式得到πr2=25π,解得r=5,然后利用勾股定理计算出圆锥的高,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算它的侧面积.
解答:解:设圆锥的底面圆的半径为r,
则πr2=25π,解得r=5,
所以圆锥的高=
=12(cm),
圆锥的侧面积=
•2π•5•13=65π(cm2).
故答案为12cm,65πcm2.
则πr2=25π,解得r=5,
所以圆锥的高=
| 132-52 |
圆锥的侧面积=
| 1 |
| 2 |
故答案为12cm,65πcm2.
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,把一张三角形纸片ABC沿中位线DE剪开后,在平面上将△ADE绕着点E顺时针旋转180°,点D到了点F的位置,则S△ADE:S?BCFD是( )
如图,把一张三角形纸片ABC沿中位线DE剪开后,在平面上将△ADE绕着点E顺时针旋转180°,点D到了点F的位置,则S△ADE:S?BCFD是( )| A、1:4 | B、1:3 |
| C、1:2 | D、1:1 |
直角三角形的两直角边分别为5厘米、12厘米,则斜边上的高是( )
| A、6厘米 | ||
| B、8厘米 | ||
C、
| ||
D、
|
 如图,OA是⊙O的半径,以OA为直径作⊙O′,⊙O的半径OC交⊙O′于点B,则
如图,OA是⊙O的半径,以OA为直径作⊙O′,⊙O的半径OC交⊙O′于点B,则 |
| AC |
 |
| AB |
| A、两弧所含的度数相等 |
| B、两弧是等弧 |
| C、两弧的长度相等 |
| D、弧AC的长度大 |
 如图,这是一所学校的平面示意图(图中小正方形的边长代表100m).请你建立适当的平面直角坐标系,写出宿舍楼、教学楼、体育馆、校门、办公楼、实验楼的位置.
如图,这是一所学校的平面示意图(图中小正方形的边长代表100m).请你建立适当的平面直角坐标系,写出宿舍楼、教学楼、体育馆、校门、办公楼、实验楼的位置.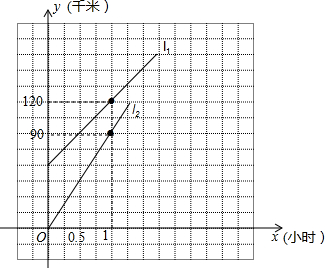 王经理从办公室乘A车去某市参加会议,开车50分钟后,发现有一重要文件遗漏在办公室中,他立即打电话通知秘书,让他拿着文件开车送往开会地点,10分钟后秘书乘B车开始按王经理乘车路线追赶,如图所示的l1和l2表示A、B两车相对于出发地的距离y(千米)与追赶时间x(小时)之间的关系:
王经理从办公室乘A车去某市参加会议,开车50分钟后,发现有一重要文件遗漏在办公室中,他立即打电话通知秘书,让他拿着文件开车送往开会地点,10分钟后秘书乘B车开始按王经理乘车路线追赶,如图所示的l1和l2表示A、B两车相对于出发地的距离y(千米)与追赶时间x(小时)之间的关系: