题目内容
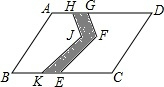 如图,在平行四边形ABCD这块土地上,有一条小路(阴影部分),现要把它改为经过点E的直路,并保持小路两侧土地的面积不变,请在图中画出你设计的小路,并说明理由.
如图,在平行四边形ABCD这块土地上,有一条小路(阴影部分),现要把它改为经过点E的直路,并保持小路两侧土地的面积不变,请在图中画出你设计的小路,并说明理由.考点:作图—应用与设计作图
专题:
分析:首先连接EG,过点F作EG的平行线交BC于点N,根据三角形面积关系,只要证明△EIN面积等于△GIF面积,即可解决问题.
解答: 解:连接EG,过点F作EG的平行线交BC于点N.连接GN,GN就是所取直的小路.
解:连接EG,过点F作EG的平行线交BC于点N.连接GN,GN就是所取直的小路.
理由如下:设GN交FE于点I,在梯形FNGE中,点I是它的对角线的交点,
故△EIN的面积等于△GIF的面积,(同底等高).
把两个三角形面积都减去△FIN面积,
所以△EIN面积等于△GIF面积,即小路两侧土地面积都不变.
 解:连接EG,过点F作EG的平行线交BC于点N.连接GN,GN就是所取直的小路.
解:连接EG,过点F作EG的平行线交BC于点N.连接GN,GN就是所取直的小路.理由如下:设GN交FE于点I,在梯形FNGE中,点I是它的对角线的交点,
故△EIN的面积等于△GIF的面积,(同底等高).
把两个三角形面积都减去△FIN面积,
所以△EIN面积等于△GIF面积,即小路两侧土地面积都不变.
点评:此题考查的是面积及等积变换,能根据题意作出辅助线,构造出面积相等的三角形是解答此题的关键.

练习册系列答案
相关题目
 如图,OA是⊙O的半径,以OA为直径作⊙O′,⊙O的半径OC交⊙O′于点B,则
如图,OA是⊙O的半径,以OA为直径作⊙O′,⊙O的半径OC交⊙O′于点B,则 |
| AC |
 |
| AB |
| A、两弧所含的度数相等 |
| B、两弧是等弧 |
| C、两弧的长度相等 |
| D、弧AC的长度大 |
 如图,这是一所学校的平面示意图(图中小正方形的边长代表100m).请你建立适当的平面直角坐标系,写出宿舍楼、教学楼、体育馆、校门、办公楼、实验楼的位置.
如图,这是一所学校的平面示意图(图中小正方形的边长代表100m).请你建立适当的平面直角坐标系,写出宿舍楼、教学楼、体育馆、校门、办公楼、实验楼的位置. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,以直角顶点C为旋转中心,将△ABC逆时针旋转到△A′B′C的位置,其中A′,B′分别是A,B的对应点,当点B′,C,A在一条直线上时,∠A′BA的度数为( )
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,以直角顶点C为旋转中心,将△ABC逆时针旋转到△A′B′C的位置,其中A′,B′分别是A,B的对应点,当点B′,C,A在一条直线上时,∠A′BA的度数为( )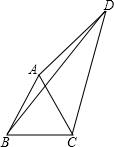 在四边形ABCD中,△ABC是等边三角形,∠ADC=30°,AD=3,BD=2
在四边形ABCD中,△ABC是等边三角形,∠ADC=30°,AD=3,BD=2 已知AB是⊙O的直径,AD与⊙O相交,点C是⊙O上一点,经过点C的直线交AD于点E,如图.若CE是⊙O的切线,AC平分∠BAD,AB=8,AC=6.求AD的长.
已知AB是⊙O的直径,AD与⊙O相交,点C是⊙O上一点,经过点C的直线交AD于点E,如图.若CE是⊙O的切线,AC平分∠BAD,AB=8,AC=6.求AD的长. 如图,已知AB是⊙O的直径,C,D是圆上两点,且
如图,已知AB是⊙O的直径,C,D是圆上两点,且