题目内容
 已知,如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C,求证:AC∥OE.
已知,如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C,求证:AC∥OE.考点:切线的性质
专题:证明题
分析:由切线长定理可知CE=BE,∠CED=∠BED,所以ED⊥BC,进而可得∠ABC+∠DOB=90°,再由圆周角定理可得∠A+∠ABC=90°,所以∠A=∠DOB,由此可得AC∥OE.
解答:证明:∵EB,EC分别切⊙O于点B,C,
∴CE=BE,∠CED=∠BED,
∴ED⊥BC,
∴∠ABC+∠DOB=90°,
∵AB为⊙O的直径,
∴A+∠ABC=90°,
∴∠A=∠DOB,
∴AC∥OE.
∴CE=BE,∠CED=∠BED,
∴ED⊥BC,
∴∠ABC+∠DOB=90°,
∵AB为⊙O的直径,
∴A+∠ABC=90°,
∴∠A=∠DOB,
∴AC∥OE.
点评:本题考查了切线长定理、圆周角定理:直径所对的圆周角是直角以及平行线的判定,题目综合性较强,难度中等.

练习册系列答案
相关题目
 如图,把一张三角形纸片ABC沿中位线DE剪开后,在平面上将△ADE绕着点E顺时针旋转180°,点D到了点F的位置,则S△ADE:S?BCFD是( )
如图,把一张三角形纸片ABC沿中位线DE剪开后,在平面上将△ADE绕着点E顺时针旋转180°,点D到了点F的位置,则S△ADE:S?BCFD是( )| A、1:4 | B、1:3 |
| C、1:2 | D、1:1 |
下列所画的数轴中正确的是( )
A、 |
B、 |
C、 |
D、 |
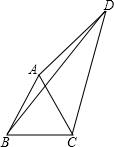 在四边形ABCD中,△ABC是等边三角形,∠ADC=30°,AD=3,BD=2
在四边形ABCD中,△ABC是等边三角形,∠ADC=30°,AD=3,BD=2