题目内容
已知一个圆柱的面积是168π，高为8，求该圆柱的底面直径．
考点：认识立体图形
专题：
分析：根据圆柱的表面积等于圆柱的侧面积加圆柱的底面积，可得答案．
解答：解：设圆柱的底面半径为r，圆柱的底面积是πr2，圆柱的侧面积是2×8πr，
由题意得
2πr2+2×8πr=168π．
化简，得r2+8r-84=0
解得r=6或r=-14（不符合题意的要舍去），
d=2r=2×6=12，
答：该圆柱的底面直径12．
由题意得
2πr2+2×8πr=168π．
化简，得r2+8r-84=0
解得r=6或r=-14（不符合题意的要舍去），
d=2r=2×6=12，
答：该圆柱的底面直径12．
点评：本题考查了认识立体图形，利用了圆柱的表面积等于圆柱的底面积加圆柱的侧面积得出方程式解题关键．
练习册系列答案
相关题目
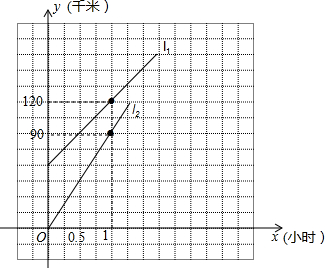王经理从办公室乘A车去某市参加会议，开车50分钟后，发现有一重要文件遗漏在办公室中，他立即打电话通知秘书，让他拿着文件开车送往开会地点，10分钟后秘书乘B车开始按王经理乘车路线追赶，如图所示的l1和l2表示A、B两车相对于出发地的距离y（千米）与追赶时间x（小时）之间的关系：
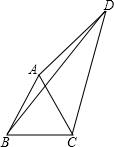在四边形ABCD中，△ABC是等边三角形，∠ADC=30°，AD=3，BD=2
如图，已知AB是⊙O的直径，C，D是圆上两点，且