题目内容
1. 阅读并填空:
阅读并填空:如图,六年级第二学期我们已经学过用直尺、圆规作线段中点的方法:
(1)以点A为圆心,以大于$\frac{1}{2}$AB的长a为半径作弧;以点B为圆心,以a为半径作弧,两弧分别相交于点E、F;
(2)作直线EF,交线段AB于点C.点C就是所求线段AB的中点,并说明这种做法正确的理由.
解:连接AE、BE、AF、BF.
在△AEF和△BEF中,
EF=EF(公共边),
AE=BE(画弧时所取的半径相等),
AF=BF(画弧时所取的半径相等).
所以△AEF≌△BEF (SSS).
所以∠AEF=∠BEF (全等三角形的对应角相等).
又因为AE=BE,
所以AC=BC (等腰三角形三线合一).
即点C是线段AB的中点.
分析 根据SSS证△AEF≌△BEF,推出∠AEF=∠BEF,根据等腰三角形性质求出即可.
解答 解:在△AEF和△BEF中,
$\left\{\begin{array}{l}{EF=EF}\\{AE=BE}\\{AF=BF}\end{array}\right.$,
∴△AEF≌△BEF(SSS),
∴∠AEF=∠BEF(全等三角形的对应角相等),
∵AE=BE,
∴AC=BC(等腰三角形的三线合一),
∴C是线段AB的中点.
故答案为:公共边,AE、BE,AF、BF,S.S.S,全等三角形对应角相等,等腰三角形三线合一.
点评 本题主要考查对等腰三角形的性质,全等三角形的性质和判定等知识点的理解和掌握,能推出∠AEF=∠BEF是解此题的关键.

练习册系列答案
相关题目
11. 如图,△ABC中,点D,E分别在边AB,BC上,DE∥AC.若BD=4,DA=2,BE=3,则BC=( )
如图,△ABC中,点D,E分别在边AB,BC上,DE∥AC.若BD=4,DA=2,BE=3,则BC=( )
 如图,△ABC中,点D,E分别在边AB,BC上,DE∥AC.若BD=4,DA=2,BE=3,则BC=( )
如图,△ABC中,点D,E分别在边AB,BC上,DE∥AC.若BD=4,DA=2,BE=3,则BC=( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{7}{2}$ | D. | $\frac{9}{2}$ |
9.下列说法中:①在Rt△ABC中,∠C=90°,CD为AB边上的中线,若CD=2,则AB=4;②八边形的内角和度数为1080°;③2、3、4、3这组数据的方差为0.5;④分式方程$\frac{1}{x}$=$\frac{3x-1}{x}$的解为x=$\frac{2}{3}$;⑤已知菱形的一个内角为60°,一条对角线为2,则另一对角线为2$\sqrt{3}$.正确的序号有( )
| A. | ①②③⑤ | B. | ①②③④ | C. | ①③④⑤ | D. | ②③④⑤ |
6.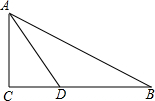 如图,在△ABC中,∠C=90°,AD平分∠BAC与BC边交于点D,BD=2CD,若点D到AB的距离等于5cm,则BC的长为( )
如图,在△ABC中,∠C=90°,AD平分∠BAC与BC边交于点D,BD=2CD,若点D到AB的距离等于5cm,则BC的长为( )
 如图,在△ABC中,∠C=90°,AD平分∠BAC与BC边交于点D,BD=2CD,若点D到AB的距离等于5cm,则BC的长为( )
如图,在△ABC中,∠C=90°,AD平分∠BAC与BC边交于点D,BD=2CD,若点D到AB的距离等于5cm,则BC的长为( )| A. | 5 | B. | 10 | C. | 15 | D. | 无法确定 |
13. 如图,在四边形ABCD中,EF∥AD∥BC,若AD=12,BC=18,且AE:EB=3:2,则EF=( )
如图,在四边形ABCD中,EF∥AD∥BC,若AD=12,BC=18,且AE:EB=3:2,则EF=( )
 如图,在四边形ABCD中,EF∥AD∥BC,若AD=12,BC=18,且AE:EB=3:2,则EF=( )
如图,在四边形ABCD中,EF∥AD∥BC,若AD=12,BC=18,且AE:EB=3:2,则EF=( )| A. | 16 | B. | 15.8 | C. | 15.6 | D. | 15.4 |
10.要使分式$\frac{1-x}{x-2}$有意义,则x应满足( )
| A. | x≠1 | B. | x≠2 | C. | x=2 | D. | x=1 |
11.把分式$\frac{x-y}{{x}^{2}-{y}^{2}}$中的x、y都扩大3倍,那么分式的值( )
| A. | 扩大3倍 | B. | 缩小为原来的$\frac{1}{3}$ | C. | 不变 | D. | 缩小为原来的$\frac{1}{9}$ |
 在平面直角坐标系中,已知直线y1=$-\frac{2}{3}$x+2与x轴、y轴分别交于点A和点B,直线y2=kx+b(k≠0)与x轴交于点C(1,0),且与线段AB相交于点P,并把△ABO分成两部分.
在平面直角坐标系中,已知直线y1=$-\frac{2}{3}$x+2与x轴、y轴分别交于点A和点B,直线y2=kx+b(k≠0)与x轴交于点C(1,0),且与线段AB相交于点P,并把△ABO分成两部分. 如图,菱形ABCD的周长为36cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于$\frac{9}{2}$cm.
如图,菱形ABCD的周长为36cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长等于$\frac{9}{2}$cm.