题目内容
8.在平面直角坐标系xOy中,抛物线y=x2-2mx+m2+m的顶点为C.(1)求点C的坐标(用含m的代数式表示)
(2)直线y=x+2与抛物线交于A、B两点,点A在抛物线的对称轴左侧.
①若P为直线OC上一动点,求△APB的面积;
②在线段AB上找一点P,连接CP,点Q从点C出发沿线段CP以每秒1个长度单位前进,然后沿线段PB以每秒$\sqrt{2}$个长度单位前进到点B,从点C出发到点B最少用时4秒,最少用时的总行程为2$\sqrt{2}$+2个长度单位.
分析 (1)把函数解析式整理成顶点式形式,然后写出点C的坐标;
(2)①联立直线与抛物线求出交点A、B的坐标,然后求出AB的长,再根据AB∥OC求出两平行线间的距离,最后根据三角形的面积公式列式计算即可得解;
②PB用时为t1=$\frac{PB}{\sqrt{2}}$=BM=PM,PC用时为:t=PC,得到t总=PM+PC=yB-yC=(m+4)-m=4s,S总=2$\sqrt{2}$+2.
解答 解:(1)∵y=x2-2mx+m2+m=(x-m)2+m,
∴顶点坐标为C(m,m);
(2)①∵y=x+2与抛物线y=x2-2mx+m2+m交于A、B两点,
∴联立$\left\{\begin{array}{l}{y={x}^{2}-2mx+{m}^{2}+m}\\{y=x+2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=m-1}\\{y=m+1}\end{array}\right.$或$\left\{\begin{array}{l}{x=m+2}\\{y=m+4}\end{array}\right.$,
∵点A在点B的左侧,
∴A(m-1,m+1),B(m+2,m+4),
∴AB=$\sqrt{(m-1-m-2)^{2}+(m+1-m-4)^{2}}$=3$\sqrt{2}$,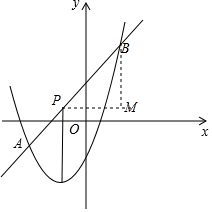
∵直线OC的解析式为y=x,直线AB的解析式为y=x+2,
∴AB∥OC,两直线AB、OC之间距离h=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
∴S△APB=$\frac{1}{2}$AB•h=$\frac{1}{2}$×3$\sqrt{2}$×$\sqrt{2}$=3;
②PB用时为t1=$\frac{PB}{\sqrt{2}}$=BM=PM,
PC用时为:t=PC,
t总=PM+PC=yB-yC=(m+4)-m=4s,
此时xp=xc=m,yp=m+2,
∴PB=2$\sqrt{2}$,PC=2,
∴S总=2$\sqrt{2}$+2,
即从点C出发到点B最少用时4秒,最少用时的总行程为2$\sqrt{2}$+2个长度单位.
故答案为:4,2$\sqrt{2}$+2.
点评 本题考查了二次函数的性质,一次函数图象上点的坐标特征,两点间的距离,三角形面积的计算,熟练掌握二次函数的性质是解题的关键.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案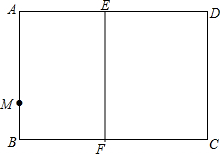 如图,在矩形纸片ABCD中,AB=4,BC=5,点E在AD边上,EF⊥BC,垂足为F,点M在AB边上,BM=1,沿过点M的直线折叠该纸片,使点A落在线段EF上的点A'处,折痕为 MN,点N在AD边上.
如图,在矩形纸片ABCD中,AB=4,BC=5,点E在AD边上,EF⊥BC,垂足为F,点M在AB边上,BM=1,沿过点M的直线折叠该纸片,使点A落在线段EF上的点A'处,折痕为 MN,点N在AD边上. 如图,在△ABC中,DE∥BC中,AD=1,BD=2,DE=2,求BC的长.
如图,在△ABC中,DE∥BC中,AD=1,BD=2,DE=2,求BC的长. 在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).
在边长为1的小正方形组成的正方形网格中建立如图所示的平面直角坐标系,已知格点三角形ABC(三角形的三个顶点都在小正方形的顶点上).
 如图,已知:AO=BO,OC=OD.求证:∠ADC=∠BCD.
如图,已知:AO=BO,OC=OD.求证:∠ADC=∠BCD. 如图,点A、B、D、C都在圆上$\widehat{BD}$=$\widehat{DC}$,AD与BC相交于点E.
如图,点A、B、D、C都在圆上$\widehat{BD}$=$\widehat{DC}$,AD与BC相交于点E. 如图,直线l1过点A(0,-5),点B(5,0),直线l2与x轴交于点C(-1,0),与y轴交于点D(0,-1),两直线l1,l2相交于点P,求△PAD的面积是4.
如图,直线l1过点A(0,-5),点B(5,0),直线l2与x轴交于点C(-1,0),与y轴交于点D(0,-1),两直线l1,l2相交于点P,求△PAD的面积是4.