题目内容
17. 如图,点A、B、D、C都在圆上$\widehat{BD}$=$\widehat{DC}$,AD与BC相交于点E.
如图,点A、B、D、C都在圆上$\widehat{BD}$=$\widehat{DC}$,AD与BC相交于点E.(1)图中一共有3对相似三角形;
(2)若AB=6,AC=4,AE=3,试求AD、CD的长.
分析 (1)由圆周角定理容易得出结论;
(2)由相似三角形的对应边成比例求出AD,得出DE,即可求出CD的长.
解答 解:(1)图中一共有3对相似三角形;理由如下:
∵$\widehat{BD}$=$\widehat{DC}$,
∴∠BAD=∠BCD=∠DAC,
∵∠B=∠D,
∴△ABE∽△CDE∽△ADC,图中共有3对相似三角形,
故答案为:3;
(2)∵△ABE∽△ADC∽△CDE,
∴$\frac{AB}{AD}=\frac{AE}{AC}$,$\frac{CD}{DE}=\frac{AD}{CD}$,
即$\frac{6}{AD}=\frac{3}{4}$,
解得:AD=8,
∴DE=AD-AE=5,
∴$\frac{CD}{5}=\frac{8}{CD}$,
解得:CD=2$\sqrt{10}$.
点评 本题考查了相似三角形的判定与性质、圆周角定理;熟练掌握圆周角定理,证明三角形相似是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知△ABC内接于圆O,$\widehat{AB}$=$\widehat{AC}$,tanB=$\frac{1}{2}$,求$\frac{AB}{BC}$的值.
如图,已知△ABC内接于圆O,$\widehat{AB}$=$\widehat{AC}$,tanB=$\frac{1}{2}$,求$\frac{AB}{BC}$的值.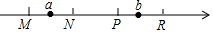 如图M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1,数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=2,则原点是N或P(填入M、N、P、R中的一个或几个).
如图M,N,P,R分别是数轴上四个整数所对应的点,其中有一点是原点,并且MN=NP=PR=1,数a对应的点在M与N之间,数b对应的点在P与R之间,若|a|+|b|=2,则原点是N或P(填入M、N、P、R中的一个或几个).