题目内容
13.计算:($\sqrt{3}$-$\sqrt{2}$)($\sqrt{2}$-$\sqrt{3}$)-6$\sqrt{\frac{2}{3}}$.解方程组 $\left\{\begin{array}{l}{x-y=4}\\{2x+y=5}\end{array}\right.$.
分析 (1)先利用完全平方公式计算,然后化简后合并即可;
(2)利用加减消元法解方程组.
解答 解:(1)原式=-($\sqrt{3}$-$\sqrt{2}$)2-2$\sqrt{6}$
=-(3-2$\sqrt{6}$+2)-2$\sqrt{6}$
=-5+2$\sqrt{6}$-2$\sqrt{6}$
=-5;
(2)$\left\{\begin{array}{l}{x-y=4①}\\{2x+y=5②}\end{array}\right.$,
①+②得3x=9,解得x=3,
把x=3代入①得3-y=4,解得y=-1,
所以方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$.
点评 本题考查了二次根式的混合运算:还涉及到二元一次方程组的解法,先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
3. 如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )
如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )
 如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )
如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
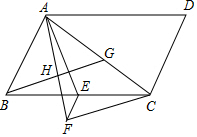 在平行四边形ABCD中,AC是对角线,∠ACD=90°.点E是BC的中点,AF平分∠BAC,CF⊥AF于点F.连接EF.
在平行四边形ABCD中,AC是对角线,∠ACD=90°.点E是BC的中点,AF平分∠BAC,CF⊥AF于点F.连接EF.