题目内容
9. 如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.
如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.(1)求证:FB2=FE•FA;
(2)若BF=3,EF=2,求△ABE与△BEF的面积之比.
分析 (1)要证明FB2=FE•FA,只要证明△FBE∽△FAB即可,根据题目中的条件可以找到两个三角形相似的条件,本题得以解决;
(2)根据(1)中的结论可以得到AE的长,然后根据△ABE与△BEF如果底边分别为AE和EF,则底边上的高相等,面积之比就是AE和EF的比值.
解答 (1)证明:∵AB∥CD,
∴∠A=∠D.
又∵∠CBF=∠D,
∴∠A=∠CBF,
∵∠BFE=∠AFB,
∴△FBE∽△FAB,
∴$\frac{FB}{FA}=\frac{FE}{FB}$
∴FB2=FE•FA;
(2)∵FB2=FE•FA,BF=3,EF=2
∴32=2×(2+AE)
∴$AE=\frac{5}{2}$
∴$\frac{AE}{EF}=\frac{5}{4}$,
∴△ABE与△BEF的面积之比为5:4.
点评 本题考查相似三角形的判定与性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
相关题目
14.下列计算正确的是( )
| A. | a6÷a2=a3 | B. | a•a=2a | C. | (a4)3=a12 | D. | a2+a2=2a4 |
1.Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,r为半径作⊙C,则正确的是( )
| A. | 当r=2时,直线AB与⊙C相交 | B. | 当r=3时,直线AB与⊙C相离 | ||
| C. | 当r=2.4时,直线AB与⊙C相切 | D. | 当r=4时,直线AB与⊙C相切 |
18.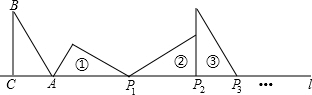 如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此顺序继续旋转,得到点P2016,则AP2016=( )
如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此顺序继续旋转,得到点P2016,则AP2016=( )
 如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此顺序继续旋转,得到点P2016,则AP2016=( )
如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上,将△ABC绕点A顺时针转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此顺序继续旋转,得到点P2016,则AP2016=( )| A. | 2016+671$\sqrt{3}$ | B. | 2016+672$\sqrt{3}$ | C. | 2017+672$\sqrt{3}$ | D. | 2016+673$\sqrt{3}$ |
 如图,一张长3x的正方形纸片,剪去两个一样的小直角三角形和一个长方形.设剪去的小长方形的长和宽分别为x,y,剪去的两个小直角三角形直角边的长也分别为x,y.
如图,一张长3x的正方形纸片,剪去两个一样的小直角三角形和一个长方形.设剪去的小长方形的长和宽分别为x,y,剪去的两个小直角三角形直角边的长也分别为x,y. 如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°10′,则∠AOB的度数为100°40′.
如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°10′,则∠AOB的度数为100°40′.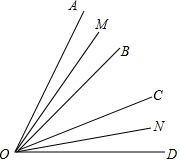 如图,OB、OC是∠AOD的两条射线,OM和ON分别是∠AOB和∠COD内部的一条射线,且∠AOD=α,∠MON=β.
如图,OB、OC是∠AOD的两条射线,OM和ON分别是∠AOB和∠COD内部的一条射线,且∠AOD=α,∠MON=β.