题目内容
20.从一张边长分别为3cm、4cm、5cm的三角形纸片中剪出一个面积最大的圆,这个圆的半径为1cm.分析 先利用勾股定理的逆定理判断这个三角形为直角三角形,然后根据直角三角形的内切圆的半径r=$\frac{a+b-c}{2}$可计算出为三角形的内切圆为1cm,于是可判断面积最大的圆的半径为1cm.
解答 解:∵32+42=52,
∴这个三角形为直角三角形,
∵三角形中面积最大的圆为三角形的内切圆,
而这个内切圆的半径=$\frac{3+4-5}{2}$=1,
即面积最大的圆的半径为1cm.
故答案为1.
点评 本题考查了三角形内切圆与内心:三角形的内心就是三角形三个内角角平分线的交点.三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.记住直角三角形的内切圆的半径r=$\frac{a+b-c}{2}$(其中a、b为直角边,c为斜边).

练习册系列答案
相关题目
8.把两张同样的长方形纸,卷成形状不同的圆柱筒,并装上两个底面,那么做成的两个圆柱体( )
| A. | 表面积一定相等 | B. | 体积一定相等 | C. | 侧面积一定相等 | D. | 底面积一定相等 |
15.2016年12月16日央视新闻报道:“不施肥不打药,袁隆平用海水种出红色水稻-海稻86”.其科研组在研究过程中,将“海稻86”在不同条件的甲、乙两块试验田进行试验,得到每块试验田每亩产量的两组数据,其方差分别为s2甲=0.002,s2乙=0.03,则( )
| A. | 甲比乙的产量稳定 | B. | 乙比甲的产量稳定 | ||
| C. | 甲、乙的产量一样稳定 | D. | 无法确定哪一品种的产量更稳定 |
12.黄金分割比在实际生活中有广泛的应用,比如在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感,按此比例,如果雕像的高为2m,它的下部为x米,则下列关于x的方程正确的是( )
| A. | x2+2x-4=0 | B. | x2-2x-4=0 | C. | x2-6x+4=0 | D. | x2-6x-4=0 |
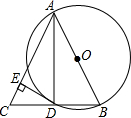 已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连结AC,过点D作DE⊥AC,垂足为E.
已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连结AC,过点D作DE⊥AC,垂足为E.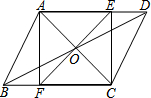 在?ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC.
在?ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC. 如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.
如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.