题目内容
1.Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,r为半径作⊙C,则正确的是( )| A. | 当r=2时,直线AB与⊙C相交 | B. | 当r=3时,直线AB与⊙C相离 | ||
| C. | 当r=2.4时,直线AB与⊙C相切 | D. | 当r=4时,直线AB与⊙C相切 |
分析 过C作CD⊥AB于D,根据勾股定理求出AB,根据三角形面积公式求出CD,和⊙C的半径比较即可.
解答 
解:过C作CD⊥AB于D,
在Rt△ACB中,由勾股定理得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
由三角形面积公式得:$\frac{1}{2}$×3×4=$\frac{1}{2}$×5×CD,
CD=2.4,
即C到AB的距离等于⊙C的半径长,
∴⊙C和AB的位置关系是相切,
故选C.
点评 本题考查了直线与圆的位置关系的应用,注意:直线和圆有三种位置关系:相切、相交、相离.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
12.黄金分割比在实际生活中有广泛的应用,比如在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感,按此比例,如果雕像的高为2m,它的下部为x米,则下列关于x的方程正确的是( )
| A. | x2+2x-4=0 | B. | x2-2x-4=0 | C. | x2-6x+4=0 | D. | x2-6x-4=0 |
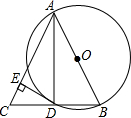 已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连结AC,过点D作DE⊥AC,垂足为E.
已知:AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使AB=AC,连结AC,过点D作DE⊥AC,垂足为E. 如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.
如图,已知AB∥CD,AD、BC相交于点E,点F在ED上,且∠CBF=∠D.