Question

2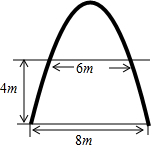．如图是抛物线形拱桥，原来水面宽为8米，后来因为涨潮，水面升高了4米，此时水面宽为6米，试求此时拱顶离水面的高度．（精确到0.1m）

Answer 1

分析 根据已知得出直角坐标系，进而求出二次函数解析式，再根据通过把x=0代入抛物线解析式得出此时拱顶离水面的高度．

解答 解：建立如图所示的平面直角坐标系．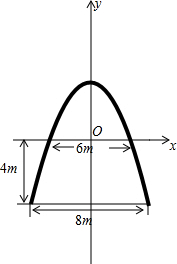

该抛物线经过点（-4，-8），与x轴的交点坐标是（-3，0）、（3，0）．
故设该抛物线解析式为：y=a（x+3）（x-3）（a≠0）．
把点（-4，-8）代入，得
a（-4+3）（-4-3）=-8，
解得a=-$\frac{8}{7}$．
则该抛物线解析式为y=-$\frac{8}{7}$（x+3）（x-3）．
把x=0代入，得到：y=-$\frac{8}{7}$（0+3）（0-3）=$\frac{72}{7}$≈10.3（m）．
答：此时拱顶离水面的高度约为10.3m．

点评 此题主要考查了二次函数的应用，根据已知建立坐标系从而得出二次函数解析式是解决问题的关键．