题目内容
12. 如图,在△ABC中,∠B=2∠C,BC═2AB,AD是中线,求证:△ABD是等边三角形.
如图,在△ABC中,∠B=2∠C,BC═2AB,AD是中线,求证:△ABD是等边三角形.
分析 根据已知条件得到AB=BD=CD,在CB的延长线上截取BE=AB,连接AE,由等腰三角形的性质得到∠E=∠BAE,得到∠E=∠C,由等腰三角形的判定得到AE=AC,
根据全等三角形的性质得到AB=AD,根据得到结论.
解答  证明:∵BC=2AB,AD是BC边的中线,
证明:∵BC=2AB,AD是BC边的中线,
∴AB=BD=CD,
在CB的延长线上截取BE=AB,连接AE
则∠E=∠BAE,
∵∠B=∠E+∠BAE=2∠E,∠B=2∠C,
∴∠E=∠C,
∴AE=AC,
在△ADE与△ABC中,$\left\{\begin{array}{l}{AE=AC}\\{∠E=∠C}\\{ED=CB}\end{array}\right.$,
∴△ABE≌△ADC(SAS),
∴AB=AD,
∴AB=BD=AD,
即△ABD是等边三角形.
点评 本题考查了等边三角形的好像和判定,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
2. 如图,AB∥CD,∠BEF的平分线交CD于点G,如果∠EFG=54°,则∠FGE的度数为( )
如图,AB∥CD,∠BEF的平分线交CD于点G,如果∠EFG=54°,则∠FGE的度数为( )
 如图,AB∥CD,∠BEF的平分线交CD于点G,如果∠EFG=54°,则∠FGE的度数为( )
如图,AB∥CD,∠BEF的平分线交CD于点G,如果∠EFG=54°,则∠FGE的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 63° |
17.如果(3+$\sqrt{3}$)2=a+b$\sqrt{3}$(a、b为实数),则a+b等于( )
| A. | 9 | B. | 18 | C. | 12 | D. | 6 |
4. 如图,平行四边形ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )
如图,平行四边形ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )
 如图,平行四边形ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )
如图,平行四边形ABCD中,△AOD可以看作是由下列哪个三角形旋转而得到的( )| A. | △AOB | B. | △DOC | C. | △BOC | D. | △BCD |
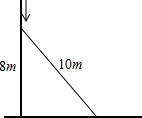 一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.
一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m.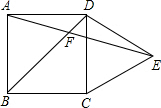 如图,在正方形ABCD外侧作等边△CDE,AE,BD相交于点F,则∠AFB=60°.
如图,在正方形ABCD外侧作等边△CDE,AE,BD相交于点F,则∠AFB=60°.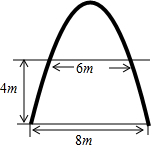 如图是抛物线形拱桥,原来水面宽为8米,后来因为涨潮,水面升高了4米,此时水面宽为6米,试求此时拱顶离水面的高度.(精确到0.1m)
如图是抛物线形拱桥,原来水面宽为8米,后来因为涨潮,水面升高了4米,此时水面宽为6米,试求此时拱顶离水面的高度.(精确到0.1m)