题目内容
17.已知|ab-2|和|b-1|互为相反数,求:(1)求a、b的值.
(2)求$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2015)(b+2015)}$的值.
分析 先根据绝对值的非负性,求得字母a和b的值,再将a和b的值代入分式,化简变形即可.
解答 解:(1)∵|ab-2|和|b-1|互为相反数,
∴|ab-2|+|b-1|=0,
即|ab-2|=0,|b-1|=0,
解得a=2,b=1;
(2)$\frac{1}{ab}$+$\frac{1}{(a+1)(b+1)}$+$\frac{1}{(a+2)(b+2)}$+…+$\frac{1}{(a+2015)(b+2015)}$
=$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2016×2017}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-…+$\frac{1}{2016}$-$\frac{1}{2017}$
=1-$\frac{1}{2017}$
=$\frac{2016}{2017}$.
点评 本题主要考查了分式求值以及绝对值的非负性的运用,解题的关键是掌握:当几个数或式的绝对值相加和为0时,则其中的每一项都必须等于0.根据此性质可列出方程求出未知数的值.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
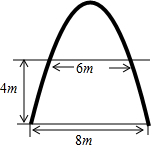 如图是抛物线形拱桥,原来水面宽为8米,后来因为涨潮,水面升高了4米,此时水面宽为6米,试求此时拱顶离水面的高度.(精确到0.1m)
如图是抛物线形拱桥,原来水面宽为8米,后来因为涨潮,水面升高了4米,此时水面宽为6米,试求此时拱顶离水面的高度.(精确到0.1m)