题目内容
7.下列式子:a+2b;$\frac{a-b}{2}$;$\frac{1}{3}$(x2-y2);$\frac{2}{a}$;0中,整式的个数是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据整式的概念进行判断即可.
解答 解:a+2b、$\frac{a-b}{2}$、$\frac{1}{3}$(x2-y2)、0是整式,
故选:C.
点评 本题考查的是整式的概念,单项式和多项式统称为整式.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
17.如果(3+$\sqrt{3}$)2=a+b$\sqrt{3}$(a、b为实数),则a+b等于( )
| A. | 9 | B. | 18 | C. | 12 | D. | 6 |
12.式子|x-2|+|x-4|+|x-4|+|x-8|的最小值是( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
2.在-1和2之间的数是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 3 |
19.已知a,b,c为△ABC的三边,a2c2+b4=a4+b2c2,则△ABC是( )
| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 等腰三角形 | D. | 等腰三角形或直角三角形 |
20.下列分式约分正确的是( )
| A. | $\frac{{a}^{6}}{{a}^{3}}$=a2 | B. | $\frac{x+y}{x-y}$=1 | C. | $\frac{2a{b}^{2}}{6{a}^{2}b}$=$\frac{1}{3}$ | D. | $\frac{m+n}{{m}^{2}+mn}$=$\frac{1}{m}$ |

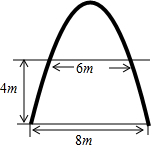 如图是抛物线形拱桥,原来水面宽为8米,后来因为涨潮,水面升高了4米,此时水面宽为6米,试求此时拱顶离水面的高度.(精确到0.1m)
如图是抛物线形拱桥,原来水面宽为8米,后来因为涨潮,水面升高了4米,此时水面宽为6米,试求此时拱顶离水面的高度.(精确到0.1m)