Question

4．在同圆或等圆中，如果圆心角∠BOA等于另一圆心角∠COD的2倍，则下列式子中一定成立的是（　　）

• A． AB=2CD
• B． $\widehat{AB}$=2$\widehat{CD}$
• C． $\widehat{AB}$＜2$\widehat{CD}$
• D． $\widehat{AB}$=$\widehat{CD}$

Answer 1

分析 取AB弧的中点E，连接AE、BE，如图，利用圆心角、弧、弦的关系得到$\widehat{AB}$=2$\widehat{CD}$，所以$\widehat{AE}$=$\widehat{BE}$=$\widehat{CD}$，则AE=BE=CD，于是根据三角形三边的关系可判断AE+BE＞AB，所以2CD＞AB．

解答 解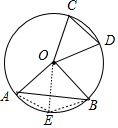：取AB弧的中点E，连接AE、BE，如图，
∵∠AOB=2∠COD，
∴$\widehat{AB}$=2$\widehat{CD}$，
∴$\widehat{AE}$=$\widehat{BE}$=$\widehat{CD}$，
∴AE=BE=CD，
而AE+BE＞AB，
∴2CD＞AB．
故选B．

点评 本题考查了圆心角、弧、弦的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．