题目内容
14.如果抛物线y=(a-3)x2-2有最低点,那么a的取值范围是a>3.分析 由于原点是抛物线y=(a+3)x2的最低点,这要求抛物线必须开口向上,由此可以确定a的范围.
解答 解:∵原点是抛物线y=(a-3)x2-2的最低点,
∴a-3>0,
即a>3.
故答案为a>3.
点评 本题主要考查二次函数的最值的知识点,解答此题要掌握二次函数图象的特点,本题比较基础.

练习册系列答案
相关题目
4.在同圆或等圆中,如果圆心角∠BOA等于另一圆心角∠COD的2倍,则下列式子中一定成立的是( )
| A. | AB=2CD | B. | $\widehat{AB}$=2$\widehat{CD}$ | C. | $\widehat{AB}$<2$\widehat{CD}$ | D. | $\widehat{AB}$=$\widehat{CD}$ |
9.已知在Rt△ABC中,∠C=90°,∠A=α,BC=2,那么AB的长等于( )
| A. | $\frac{2}{sinα}$ | B. | 2sinα | C. | $\frac{2}{cosα}$ | D. | 2cosα |
6.将抛物线y=ax2-1平移后与抛物线y=a(x-1)2重合,抛物线y=ax2-1上的点A(2,3)同时平移到A′,那么点A′的坐标为( )
| A. | (3,4) | B. | (1,2) | C. | (3,2) | D. | (1,4) |
3.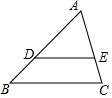 如图,点D、E位于△ABC的两边上,下列条件能判定DE∥BC的是( )
如图,点D、E位于△ABC的两边上,下列条件能判定DE∥BC的是( )
 如图,点D、E位于△ABC的两边上,下列条件能判定DE∥BC的是( )
如图,点D、E位于△ABC的两边上,下列条件能判定DE∥BC的是( )| A. | AD•DB=AE•EC | B. | AD•AE=BD•EC | C. | AD•CE=AE•BD | D. | AD•BC=AB•DE |
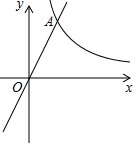 已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.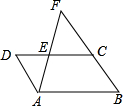 如图,已知在平行四边形ABCD中,点E是CD上一点,且DE=2,CE=3,射线AE与射线BC相交于点F;
如图,已知在平行四边形ABCD中,点E是CD上一点,且DE=2,CE=3,射线AE与射线BC相交于点F;