题目内容
12.用长度相等的小棒按下面方式搭图形
(1)搭第1个图形用12根小棒,搭第2个图形用22根小棒,搭第3个图形用42根小棒;
(2)按照这种方式搭下去,搭第4个图形用82根小棒;
(3)搭第n个图形用7+5(2n-1)根小棒.
分析 (1)根据图形可得;
(2)根据图示规律可得;
(3)由前4个图形中的数字规律可得.
解答 解:(1)图(1)中,是4×4-4=12根小棒;
图(2)中,是12+10=22根小棒;
图(3)中,是12+10×3=42根小棒;
故答案:12,22,42;
(2)按照这种方式搭下去,搭第4个图形用12+10×7=82根小棒,
故答案为:82;
(3)第n个图形需要12+10×(2n-1-1)=7+5(2n-1)根小棒,
故答案为:7+5(2n-1).
点评 本题主要考查图形的变化规律,首先正确计算前三个中的小棒根数,然后结合图形以及计算的数据发现规律.

练习册系列答案
相关题目
17. 如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
 如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )
如图,在△ABC中,AC=4cm,线段AB的垂直平分线交AC于点N,△BCN的周长是7cm,则BC的长为( )| A. | 1 cm | B. | 2 cm | C. | 3 cm | D. | 4cm |
4.在同圆或等圆中,如果圆心角∠BOA等于另一圆心角∠COD的2倍,则下列式子中一定成立的是( )
| A. | AB=2CD | B. | $\widehat{AB}$=2$\widehat{CD}$ | C. | $\widehat{AB}$<2$\widehat{CD}$ | D. | $\widehat{AB}$=$\widehat{CD}$ |
 如图,有理数a、b、c在数轴上的位置大致如下:
如图,有理数a、b、c在数轴上的位置大致如下: 如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从O点开始沿OA边向点A以1cm/s的速度移动,点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P、Q同时出发,用t(单位:秒)表示移动的时间(0≤t≤6),那么:
如图,在平面直角坐标系中,已知OA=12cm,OB=6cm,点P从O点开始沿OA边向点A以1cm/s的速度移动,点Q从点B开始沿BO边向点O以1cm/s的速度移动,如果P、Q同时出发,用t(单位:秒)表示移动的时间(0≤t≤6),那么: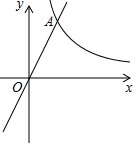 已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
已知:如图,在平面直角坐标系xOy中,反比例函数y=$\frac{8}{x}$的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.