题目内容
19. 如图,已知:AB为⊙O的直径,过A作弦AC、AD,并延长与过B的切线交于M、N,求证:∠MCN=∠MDN.
如图,已知:AB为⊙O的直径,过A作弦AC、AD,并延长与过B的切线交于M、N,求证:∠MCN=∠MDN.
分析 连接BC、BD,由勾股定理和相似得:BM2=AM•MC=AM2-AB2,化简得AB2=AM•AC,同理得:AB2=AN•AD,则AM•AC=AN•AD,证明△MAD∽△NAC,可得结论;也可以直接利用切割线定理和四点共圆来证明.
解答 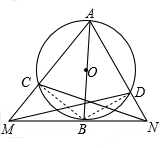 证明:连接BC、BD,
证明:连接BC、BD,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BCM=90°,
∵MN是⊙O的切线,
∴∠ABM=90°,
∴∠BCM=∠ABM,
∵∠BMC=∠BMC,
∴△BMC∽△AMB,
∴$\frac{BM}{AM}=\frac{MC}{BM}$,
∴BM2=AM•MC,
在Rt△ABM中,BM2=AM2-AB2,
∴AM2-AB2=MC•AM,
∴AM(AM-MC)=AB2,
∴AB2=AM•AC,
同理得:AB2=AN•AD,
∴AM•AC=AN•AD,
∴$\frac{AM}{AN}=\frac{AD}{AC}$,
∵∠MAD=∠NAC,
∴△MAD∽△NAC,
∴∠ADM=∠ACN,
∴∠MCN=∠MDN.
点评 本题考查了切线的性质、相似三角形的性质和判定,有难度,本题是利用构建相似三角形,利用相似三角形的对应角相等及等角的补角相等,使问题得以解决.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
9.关于x的一元二次方程x2+kx+4k2-3=0的两个实数根分别是x1,x2,且满足x1+x2=x1•x2,则k的值为( )
| A. | -1 | B. | $\frac{3}{4}$ | C. | -1或$\frac{3}{4}$ | D. | 不存在 |
10.已知∠A为锐角,且cosA=$\frac{12}{13}$,则sinA等于( )
| A. | $\frac{13}{12}$ | B. | $\frac{5}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |
4.在同圆或等圆中,如果圆心角∠BOA等于另一圆心角∠COD的2倍,则下列式子中一定成立的是( )
| A. | AB=2CD | B. | $\widehat{AB}$=2$\widehat{CD}$ | C. | $\widehat{AB}$<2$\widehat{CD}$ | D. | $\widehat{AB}$=$\widehat{CD}$ |
11.如果一斜坡的坡比是1:2.4,那么该斜坡坡角的余弦值是( )
| A. | $\frac{12}{5}$ | B. | $\frac{5}{12}$ | C. | $\frac{5}{13}$ | D. | $\frac{12}{13}$ |
9.已知在Rt△ABC中,∠C=90°,∠A=α,BC=2,那么AB的长等于( )
| A. | $\frac{2}{sinα}$ | B. | 2sinα | C. | $\frac{2}{cosα}$ | D. | 2cosα |
 如图,已知直线a∥b∥c,直线m交直线a、b、c于点A,B,C,直线n交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,求$\frac{DE}{EF}$的值.
如图,已知直线a∥b∥c,直线m交直线a、b、c于点A,B,C,直线n交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,求$\frac{DE}{EF}$的值.