题目内容
18.在Rt△ABC中,∠C=90°,其内切圆半径为2cm,斜边AB=10cm,那么△ABC的面积是( )| A. | 48cm2 | B. | 24cm2 | C. | 20cm2 | D. | 12cm2 |
分析 设Rt△ABC的内切圆与三边分别相切于D、E、F,连接OE、OF,则OE⊥BC,OF⊥AC,OE=OF,证出四边形OECF是正方形,得出CE=CF=OE=2cm,设AF=x,由切线长定理得出:AD=AF=xcm,则BE=BD=(10-x)cm,由勾股定理得出方程,解方程求出AC、BC,即可得出结果.
解答 解:如图所示:
设Rt△ABC的内切圆与三边分别相切于D、E、F,连接OE、OF,
则OE⊥BC,OF⊥AC,OE=OF,
∵∠C=90°,
∴四边形OECF是正方形,
∴CE=CF=OE=2cm,
设AF=x,由切线长定理得:AD=AF=xcm,
则BE=BD=(10-x)cm,
由勾股定理得:AC2+BC2=AB2,
即(x+2)2+(10-x+2)2=102,
解得:x=6,或x=4,
当x=6时,AC=8cm,BC=6cm;
当x=4时,AC=6cm,BC=8cm;
∴△ABC的面积=$\frac{1}{2}$×6×8=24(cm2);
故选:B.
点评 本题考查了三角形的内切圆与内心、正方形的判定与性质、切线长定理、勾股定理;熟练掌握切线长定理,由勾股定理得出方程是解决问题的关键.

练习册系列答案
相关题目
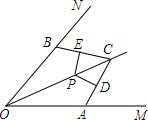 如图,OC平分∠MON,在OM、ON边上取OA=OB,点P在OC上,且PD⊥AC于D,PE⊥BC于E,求证:PD=PE.
如图,OC平分∠MON,在OM、ON边上取OA=OB,点P在OC上,且PD⊥AC于D,PE⊥BC于E,求证:PD=PE.