题目内容
16.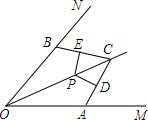 如图,OC平分∠MON,在OM、ON边上取OA=OB,点P在OC上,且PD⊥AC于D,PE⊥BC于E,求证:PD=PE.
如图,OC平分∠MON,在OM、ON边上取OA=OB,点P在OC上,且PD⊥AC于D,PE⊥BC于E,求证:PD=PE.
分析 根据OC平分∠MON,得到∠BOC=∠AOC,证得△BOC≌△AOC,根据全等三角形的性质得到∠BCO=∠ACO,根据角平分线的性质即可得到结论.
解答 证明:∵OC平分∠MON,
∴∠BOC=∠AOC,
在△BOC与△AOC中,
$\left\{\begin{array}{l}{OB=OA}\\{∠BOC=∠AOC}\\{OC=OC}\end{array}\right.$,
∴△BOC≌△AOC,
∴∠BCO=∠ACO,
∵PD⊥AC于D,PE⊥BC于E,
∴PD=PE.
点评 本题考查了全等三角形的判定和性质,角平分线的定义和性质,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
17.若(a+3)2+$\sqrt{b-2}$=0.则点P(a,b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.在Rt△ABC中,∠C=90°,其内切圆半径为2cm,斜边AB=10cm,那么△ABC的面积是( )
| A. | 48cm2 | B. | 24cm2 | C. | 20cm2 | D. | 12cm2 |
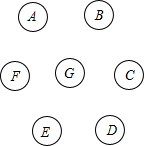 如图,一个旅游区有7个不在一条直线上的A,B,C,D,E,F,G风景点,现准备开设电车线路免费接送游客,电车线路应满足以下条件:
如图,一个旅游区有7个不在一条直线上的A,B,C,D,E,F,G风景点,现准备开设电车线路免费接送游客,电车线路应满足以下条件: 如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.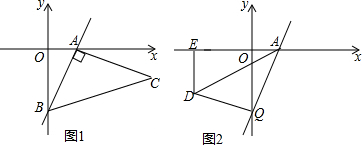
 如图,长方形ABCD中,AB=6,CB=8,点P以2个单位/s的速度从A沿AB向B运动,同时点Q以1个单位/s的速度从C沿CB向B运动,当其中的一个点到达终点时,另一个点随之停止运动,设运动时间为t s.
如图,长方形ABCD中,AB=6,CB=8,点P以2个单位/s的速度从A沿AB向B运动,同时点Q以1个单位/s的速度从C沿CB向B运动,当其中的一个点到达终点时,另一个点随之停止运动,设运动时间为t s.