题目内容
6.计算(1)|-3|-(π-1)0-($\frac{1}{2}$)-1
(2)(-xy2)3÷($\frac{1}{2}$xy2)2×$\frac{1}{2}$x
(3)(x-1)(x+3)+(2x-3y)(2x+3y)
(4)(2m+n)2-n(n+4m)-2m2.
分析 (1)根据去绝对值、零指数幂、负整数指数幂和整式的减法进行计算即可;
(2)根据积的乘方、同底数幂乘除法进行计算即可;
(3)根据多项式乘以多项式和整式的加法进行计算即可;
(4)根据完全平方和公式和整式的减法、去括号的方法进行计算即可.
解答 解:(1)|-3|-(π-1)0-($\frac{1}{2}$)-1
=3-1-$\frac{1}{\frac{1}{2}}$
=3-1-2
=0;
(2)(-xy2)3÷($\frac{1}{2}$xy2)2×$\frac{1}{2}$x
=$-{x}^{3}{y}^{6}÷\frac{1}{4}{x}^{2}{y}^{4}×\frac{1}{2}x$
=-2x2y2;
(3)(x-1)(x+3)+(2x-3y)(2x+3y)
=x2+2x-3+4x2-9y2
=5x2+2x-3-9y2;
(4)(2m+n)2-n(n+4m)-2m2
=4m2+4mn+n2-n2-4mn-2m2
=2m2.
点评 本题考查整式的混合运算、零指数幂、负整数指数幂,解题的关键是明确整式的混合运算、零指数幂、负整数指数幂的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若(a+3)2+$\sqrt{b-2}$=0.则点P(a,b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.在Rt△ABC中,∠C=90°,其内切圆半径为2cm,斜边AB=10cm,那么△ABC的面积是( )
| A. | 48cm2 | B. | 24cm2 | C. | 20cm2 | D. | 12cm2 |
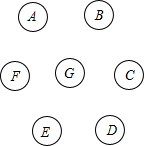 如图,一个旅游区有7个不在一条直线上的A,B,C,D,E,F,G风景点,现准备开设电车线路免费接送游客,电车线路应满足以下条件:
如图,一个旅游区有7个不在一条直线上的A,B,C,D,E,F,G风景点,现准备开设电车线路免费接送游客,电车线路应满足以下条件: